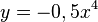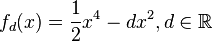Funktionenscharen: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Funktionenscharen)
(→‎Funktionenscharen)
Zeile 40: Zeile 40:
  
 
<math>f''( \sqrt d) = 6 (\sqrt d)^2-2d = 6d-2d =4d </math><br />
 
<math>f''( \sqrt d) = 6 (\sqrt d)^2-2d = 6d-2d =4d </math><br />
−
<math>f''(-\sqrt d)= 6 (-\sqrt d) ^2-2d=6d-2d=4d</math>
+
<math>f''(-\sqrt d)= 6 (-\sqrt d) ^2-2d=6d-2d=4d</math> <br />
−
<math> d < 0  \rightarrow HP </math>
+
<math> 4d > 0  \rightarrow TP </math> für beide Extrempunkte <br />
 +
für <math> d = 0 </math> liegt kein Tiefpunkt vor!
  
−
<math> d > 0 \rightarrow TP </math>
+
 
 +
<math>f''( 0) = -2d</math><br />
 +
<math> -2d < 0 \rightarrow HP </math> , für <math> d = 0 </math> liegt kein Hochpunkt vor!
  
 
== Ortskurven ==
 
== Ortskurven ==

Version vom 21. Februar 2014, 11:03 Uhr

Die folgenden Kapitel werden anhand einer Aufgabe erklärt.

30px   Aufgabe

Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte?
f_d (x)= {1 \over 2} x^4 -d x^2, d \in \mathbb{R}

Funktionenscharen

Berechnung der Extrempunkte:
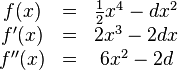
\begin{matrix} f(x)&=& {1 \over 2} x^4-dx^2 \\ f'(x)&=& 2x^3-2dx \\ f''(x)&=& 6x^2-2d \end{matrix}


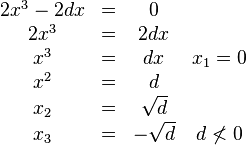
\begin{matrix} 2x^3-2dx&=& 0 & \\ 2x^3&=& 2dx &\\ x^3 &=& dx & x_1 = 0\\ x^2&=& d &\\ x_2&=& \sqrt d &\\ x_3&=& - \sqrt d & d \not< 0 \end{matrix}


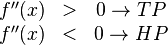
\begin{matrix} f''(x) &>& 0 \rightarrow TP \\ f''(x) &<& 0 \rightarrow HP \end{matrix}


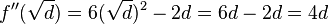
f''( \sqrt d) = 6 (\sqrt d)^2-2d = 6d-2d =4d
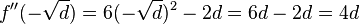
f''(-\sqrt d)= 6 (-\sqrt d) ^2-2d=6d-2d=4d
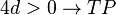4d > 0 \rightarrow TP für beide Extrempunkte
für 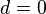d = 0 liegt kein Tiefpunkt vor!


f''( 0) = -2d
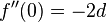
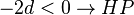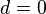-2d < 0 \rightarrow HP , für d = 0 liegt kein Hochpunkt vor!

Ortskurven

Bestimmung der Ortskurve der Hochpunkte:

Ortskurven sind Kurven, auf denen Punkte mit gleichen Eigenschaften einer Kurvenschar liegen z.B alle Hochpunkte.

Bestimmen von Ortskurven

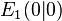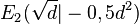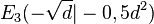
Die Koordinaten des Extrempunktes sind E_1 ( 0 | 0 ) , E_2 ( \sqrt d | - 0,5 d^2) , E_3 ( -\sqrt d | - 0,5 d^2)


Koordinaten der Extrempunkte einzeln aufschreiben:

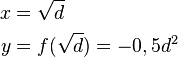
\begin{align} x&=\sqrt d \\ y&= f( \sqrt d ) = - 0,5 d^2 \end{align}


x - Koordinate nach Parameter auflösen:

d= x^2


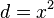
Diesen Parameter in die y - Gleichung einsetzen:

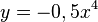
y= -0,5x^4


Gleichung der Ortskurve der Extrempunkte:

y= -0,5 x^4


Von „http://fsg.zum.de/index.php?title=Funktionenscharen&oldid=1593“