Flächenberechnung mit Hilfe des Integrals: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Einleitung === Warum lässt sich ein Flächeninhalt mit Hilfe des Integrals bestimmen? Da das Integral den Grenzwert von Ober- und Untersumme angibt lässt s…“) |
|||
| (15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
| − | |||
| + | ==== Fläche oberhalb der x-Achse ==== | ||
| + | |||
| + | [[Datei:fall1.jpg|rahmenlos|rechts]] | ||
Liegt der Graph der Funktion <math>f</math> im Intervall <math>[a;b]</math> oberhalb der <math>x</math>-Achse, so gilt die Formel <math>A= \int_{a}^{b} f(x)\, dx</math> | Liegt der Graph der Funktion <math>f</math> im Intervall <math>[a;b]</math> oberhalb der <math>x</math>-Achse, so gilt die Formel <math>A= \int_{a}^{b} f(x)\, dx</math> | ||
| − | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==== Fläche unterhalb der x-Achse ==== | ||
| + | |||
| + | [[Datei:fall2.jpg|rahmenlos|rechts]] | ||
Liegt der Graph der Funktion <math>f</math> im Intervall <math>[a;b]</math> unterhalb der <math>x</math>-Achse, so ist der Wert des Integrals negativ. | Liegt der Graph der Funktion <math>f</math> im Intervall <math>[a;b]</math> unterhalb der <math>x</math>-Achse, so ist der Wert des Integrals negativ. | ||
| Zeile 27: | Zeile 42: | ||
Da das Ergebnis negativ wäre schreibt man vor das Integral ein Minus. Flächeninhalte sind immer positiv. | Da das Ergebnis negativ wäre schreibt man vor das Integral ein Minus. Flächeninhalte sind immer positiv. | ||
Mit dem Betrag wird das gleiche bewirkt. | Mit dem Betrag wird das gleiche bewirkt. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| Zeile 32: | Zeile 54: | ||
==== Fläche ober- und unterhalb der x-Achse ==== | ==== Fläche ober- und unterhalb der x-Achse ==== | ||
| + | [[Datei:fall_3.jpg|rahmenlos|rechts]] | ||
Die Fläche liegt im Intervall <math>[a;b]</math> sowohl oberhalb als auch unterhalb der <math>x</math>-Achse (Der Graph <math>f</math> hat im Intervall <math>[a;b]</math> Nullstellen) | Die Fläche liegt im Intervall <math>[a;b]</math> sowohl oberhalb als auch unterhalb der <math>x</math>-Achse (Der Graph <math>f</math> hat im Intervall <math>[a;b]</math> Nullstellen) | ||
Das Integral von <math>a</math> nach <math>b</math> muss in zwei Integrale unterteilt werden. Die Teilflächen müssen also getrennt berechnet werden. Die Nullstellen geben hierbei jeweils die Grenzen an. | Das Integral von <math>a</math> nach <math>b</math> muss in zwei Integrale unterteilt werden. Die Teilflächen müssen also getrennt berechnet werden. Die Nullstellen geben hierbei jeweils die Grenzen an. | ||
| − | Es gilt: <math>A= \left|\int_{a}^{c} f(x)\, dx\right| +\left|\int_{ | + | Es gilt: <math>A= \left|\int_{a}^{c} f(x)\, dx\right| +\left|\int_{c}^{b} f(x)\, dx\right| </math> |
Die negativen Werte für einen Teilbereich des Integrals werden mit dem Betrag positiv gemacht. Hierbei ist darauf zu achten, dass man für jeden Summanden einen extra Betrag setzt. Zum Schluss werden alle Werte addiert. | Die negativen Werte für einen Teilbereich des Integrals werden mit dem Betrag positiv gemacht. Hierbei ist darauf zu achten, dass man für jeden Summanden einen extra Betrag setzt. Zum Schluss werden alle Werte addiert. | ||
| + | |||
| + | ---- | ||
==== Fläche zwischen zwei Graphen ==== | ==== Fläche zwischen zwei Graphen ==== | ||
| + | |||
| + | [[Datei:Fall4.jpg|rahmenlos|rechts]] | ||
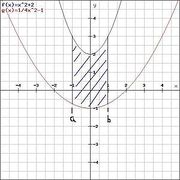
Die Fläche wird von den Graphen zweier Funktionen <math>f</math> und <math>g</math> begrenzt. Im Intervall <math>[a;b]</math> liegt sie über der <math>x</math>-Achse. | Die Fläche wird von den Graphen zweier Funktionen <math>f</math> und <math>g</math> begrenzt. Im Intervall <math>[a;b]</math> liegt sie über der <math>x</math>-Achse. | ||
Voraussetzung hierfür ist, dass <math>f(x)\ge g(x)</math> gilt. | Voraussetzung hierfür ist, dass <math>f(x)\ge g(x)</math> gilt. | ||
| Zeile 56: | Zeile 83: | ||
<math>A= \int_{a}^{b} (obere Funktion - untere Funktion)\, dx </math> | <math>A= \int_{a}^{b} (obere Funktion - untere Funktion)\, dx </math> | ||
| − | Man bestimmt also zunächst den gesamten Flächeninhalt im Intervall <math>[a;b]</math> zwischen <math>f(x)</math> und der <math>x</math>-Achse. Von diesem Wert wird nun der | + | Man bestimmt also zunächst den gesamten Flächeninhalt im Intervall <math>[a;b]</math> zwischen <math>f(x)</math> und der <math>x</math>-Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall <math>[a;b]</math> zwischen der Funktion <math>g</math> und der <math>x</math>-Achse subtrahiert. Es wird also wie oben beschrieben der Flächeninhalt der oberen Funktion minus dem Flächeninhalt der unteren Funktion gerechnet. |
| − | ==== Fläche zwischen zwei Graphen mit positiven und negativen Funktionswerten ==== | + | |
| + | ---- | ||
| + | |||
| + | ==== Fläche zwischen zwei Graphen mit positiven und negativen Funktionswerten ==== | ||
| + | |||
| + | [[Datei:fall5.jpg|rahmenlos|rechts]] | ||
Eine Fläche, die von zwei Graphen <math>f</math> und <math>g</math> begrenzt wird. Ein Graph nimmt sowohl positive wie auch negative Funktionswerte an. | Eine Fläche, die von zwei Graphen <math>f</math> und <math>g</math> begrenzt wird. Ein Graph nimmt sowohl positive wie auch negative Funktionswerte an. | ||
Hier geht man genauso vor wie beim Fall 4. | Hier geht man genauso vor wie beim Fall 4. | ||
Begründung: Der Flächeninhalt bleibt immer gleich groß, egal in welchem Quadrant/welchen Quadranten die Fläche liegt. Man darf die Graphen beliebig weit nach oben verschieben. | Begründung: Der Flächeninhalt bleibt immer gleich groß, egal in welchem Quadrant/welchen Quadranten die Fläche liegt. Man darf die Graphen beliebig weit nach oben verschieben. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
==== Flächenberechnung bei sich schneidenden Graphen ==== | ==== Flächenberechnung bei sich schneidenden Graphen ==== | ||
| + | |||
| + | [[Datei:Fall6.jpg|rahmenlos|rechts]] | ||
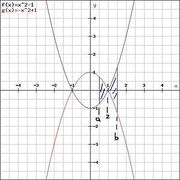
Zwei Graphen schneiden sich im Intervall <math>[a;b]</math> | Zwei Graphen schneiden sich im Intervall <math>[a;b]</math> | ||
| Zeile 85: | Zeile 130: | ||
Es gilt: | Es gilt: | ||
| − | <math>A= \int_{a}^{z} ( | + | <math>A= \int_{a}^{z} (g(x)-f(x))\, dx + \int_{z}^{b} (f(x)-g(x))\, dx</math> |
| + | |||
| + | Man geht also ähnlich wie beim Fall 4 vor. Auch hier nimmt man zuerst den gesamten Flächeninhalt im Intervall <math>[a;z]</math> zwischen der oberen Funktion <math>f(x)</math> und der <math>x</math>-Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall <math>[a;z]</math> zwischen der Funktion <math>g(x)</math> und der <math>x</math>-Achse subtrahiert. Im nächsten Schritt geht man genauso vor, nur dass nun <math>g(x)</math> die obere Funktion und <math>f(x)</math> die untere Funktion ist. | ||
| − | |||
| + | ---- | ||
| − | === Flächenberechnung mit dem GTR === | + | === Flächenberechnung mit dem GTR (TI-84 Plus) === |
''(Anleitung mit aktueller Softwareversion)'' | ''(Anleitung mit aktueller Softwareversion)'' | ||
Aktuelle Version vom 21. Mai 2015, 09:26 Uhr
Inhaltsverzeichnis |
Einleitung
Warum lässt sich ein Flächeninhalt mit Hilfe des Integrals bestimmen?
Da das Integral den Grenzwert von Ober- und Untersumme angibt lässt sich der Flächeninhalt mit Hilfe des Integrals bestimmen.
Dabei muss man beachten, dass man nicht immer einfach von der unteren Grenze 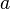 zur oberen Grenze
zur oberen Grenze 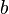 integrieren darf, wenn man den richtigen Flächeninhalt berechnen will.
integrieren darf, wenn man den richtigen Flächeninhalt berechnen will.
Die verschiedenen Fälle der Flächenberechnung:
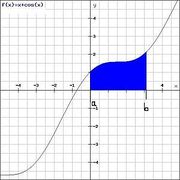
Fläche oberhalb der x-Achse
Liegt der Graph der Funktion 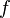 im Intervall
im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) oberhalb der
oberhalb der 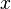 -Achse, so gilt die Formel
-Achse, so gilt die Formel 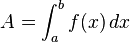
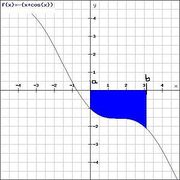
Fläche unterhalb der x-Achse
Liegt der Graph der Funktion 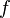 im Intervall
im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) unterhalb der
unterhalb der 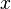 -Achse, so ist der Wert des Integrals negativ.
-Achse, so ist der Wert des Integrals negativ.
Es gilt: 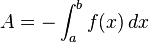 oder
oder 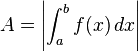
Da das Ergebnis negativ wäre schreibt man vor das Integral ein Minus. Flächeninhalte sind immer positiv. Mit dem Betrag wird das gleiche bewirkt.
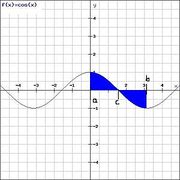
Fläche ober- und unterhalb der x-Achse
Die Fläche liegt im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) sowohl oberhalb als auch unterhalb der
sowohl oberhalb als auch unterhalb der 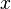 -Achse (Der Graph
-Achse (Der Graph 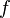 hat im Intervall
hat im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) Nullstellen)
Nullstellen)
Das Integral von 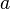 nach
nach 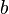 muss in zwei Integrale unterteilt werden. Die Teilflächen müssen also getrennt berechnet werden. Die Nullstellen geben hierbei jeweils die Grenzen an.
muss in zwei Integrale unterteilt werden. Die Teilflächen müssen also getrennt berechnet werden. Die Nullstellen geben hierbei jeweils die Grenzen an.
Es gilt: 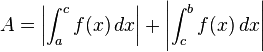
Die negativen Werte für einen Teilbereich des Integrals werden mit dem Betrag positiv gemacht. Hierbei ist darauf zu achten, dass man für jeden Summanden einen extra Betrag setzt. Zum Schluss werden alle Werte addiert.
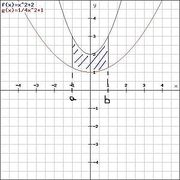
Fläche zwischen zwei Graphen
Die Fläche wird von den Graphen zweier Funktionen 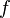 und
und 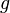 begrenzt. Im Intervall
begrenzt. Im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) liegt sie über der
liegt sie über der 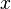 -Achse.
Voraussetzung hierfür ist, dass
-Achse.
Voraussetzung hierfür ist, dass 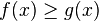 gilt.
gilt.
Es gilt: 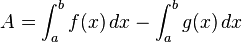
Kurzform: 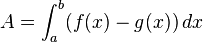
Wenn sich die Graphen von 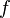 und
und 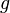 nicht schneiden gilt für den Flächeninhalt
nicht schneiden gilt für den Flächeninhalt 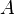 zwischen den Graphen:
zwischen den Graphen:
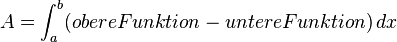
Man bestimmt also zunächst den gesamten Flächeninhalt im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) zwischen
zwischen  und der
und der 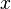 -Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall
-Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) zwischen der Funktion
zwischen der Funktion 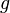 und der
und der 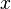 -Achse subtrahiert. Es wird also wie oben beschrieben der Flächeninhalt der oberen Funktion minus dem Flächeninhalt der unteren Funktion gerechnet.
-Achse subtrahiert. Es wird also wie oben beschrieben der Flächeninhalt der oberen Funktion minus dem Flächeninhalt der unteren Funktion gerechnet.
Fläche zwischen zwei Graphen mit positiven und negativen Funktionswerten
Eine Fläche, die von zwei Graphen 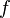 und
und 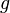 begrenzt wird. Ein Graph nimmt sowohl positive wie auch negative Funktionswerte an.
begrenzt wird. Ein Graph nimmt sowohl positive wie auch negative Funktionswerte an.
Hier geht man genauso vor wie beim Fall 4. Begründung: Der Flächeninhalt bleibt immer gleich groß, egal in welchem Quadrant/welchen Quadranten die Fläche liegt. Man darf die Graphen beliebig weit nach oben verschieben.
Flächenberechnung bei sich schneidenden Graphen
Zwei Graphen schneiden sich im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png)
Teilweise gilt 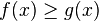 und teilweise
und teilweise 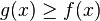 Die Intervalle müssen getrennt berechnet werden.
Die Intervalle müssen getrennt berechnet werden.
Vorgehensweise:
1. Schnittpunkt 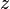 der Graphen bestimmen
der Graphen bestimmen
2. Bestimmen, in welchem Intervall 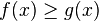 und in welchem
und in welchem 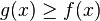 gilt
gilt
3. Berechnung des Flächeninhalts
Es gilt:
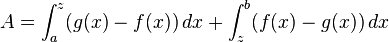
Man geht also ähnlich wie beim Fall 4 vor. Auch hier nimmt man zuerst den gesamten Flächeninhalt im Intervall ![[a;z]](/images/math/8/4/3/843254f60c297a9dc9abe958dc1a0b17.png) zwischen der oberen Funktion
zwischen der oberen Funktion  und der
und der 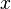 -Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall
-Achse. Von diesem Wert wird nun der Flächeninhalt im Intervall ![[a;z]](/images/math/8/4/3/843254f60c297a9dc9abe958dc1a0b17.png) zwischen der Funktion
zwischen der Funktion 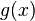 und der
und der 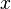 -Achse subtrahiert. Im nächsten Schritt geht man genauso vor, nur dass nun
-Achse subtrahiert. Im nächsten Schritt geht man genauso vor, nur dass nun 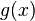 die obere Funktion und
die obere Funktion und  die untere Funktion ist.
die untere Funktion ist.
Flächenberechnung mit dem GTR (TI-84 Plus)
(Anleitung mit aktueller Softwareversion)
Am Beispiel 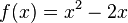
Da die Funktion auch negative Werte animmt verwendet man den Betrag der Funktion 
Anleitung (mit Zeichnung)
1. 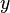 - Editor
- Editor
2. MATH - NUM: 1
3. Funktion eingeben und zeichenen lassen
4. 2nd CALC: 7
5. Grenzen eingeben
Alternativer Weg (ohne Zeichung):
1. MATH: 9
2. Grenzen eingeben
3. MATH - NUM: 1
4. Funktion eingeben und berechnen lassen