Kurvendiskussion: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(Die Seite wurde neu angelegt: „== Kriterien für Extremstellen == == Kriterien für Wendestellen == == vollständige Kurvendiskussion ==“) |
(→Kriterien für Extremstellen) |
||
| Zeile 1: | Zeile 1: | ||
== Kriterien für Extremstellen == | == Kriterien für Extremstellen == | ||
| + | ===Definition=== | ||
| + | Ein '''Hochpunkt''' hat den '''größten y-Wert in seiner Umgebung'''. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von '''positiv (+) nach negativ (-)''' . | ||
| + | Ein '''Tiefpunkt''' hat den '''kleinsten y-Wert in seiner Umgebung'''. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von '''negativ (-) nach positiv (+)''' . | ||
| + | |||
| + | ===Kriterien=== | ||
| + | # notwendige Bedingung: <math>f'(x)=0 </math> <br /> ''Begründung: Die Ableitung(Steigung) am Extrempunkt ist 0 '' | ||
| + | # hinreichende Bedingung: | ||
| + | ## schwache Bedingung: <math>f''(x)\not=0 </math> <br /> ''Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. | ||
| + | ## starke Bedingung: | ||
== Kriterien für Wendestellen == | == Kriterien für Wendestellen == | ||
Version vom 4. Dezember 2015, 10:44 Uhr
Inhaltsverzeichnis |
Kriterien für Extremstellen
Definition
Ein Hochpunkt hat den größten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von positiv (+) nach negativ (-) .
Ein Tiefpunkt hat den kleinsten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von negativ (-) nach positiv (+) .
Kriterien
- notwendige Bedingung:
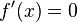
Begründung: Die Ableitung(Steigung) am Extrempunkt ist 0 - hinreichende Bedingung:
- schwache Bedingung:
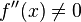
Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. - starke Bedingung:
- schwache Bedingung:

