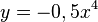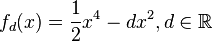Funktionenscharen: Unterschied zwischen den Versionen
(→Beispiel) |
(→Beispiel) |
||
| Zeile 95: | Zeile 95: | ||
Ortskurve bestimmen: | Ortskurve bestimmen: | ||
<br /> | <br /> | ||
| − | <math>f_t({t \over2}=(-{t \over2})^2+t | + | <math>f_t \left({t \over2}\right)=\left(-{t \over2}\right)^2+t\cdot\left(-{t \over2}\right)</math> |
<br /> | <br /> | ||
| − | <math>=(-{t \over2}) | + | <math>=\left(-{t \over2}\right)\cdot\left({t \over2}\right)+t\cdot\left({t \over2}\right)</math> |
<br /> | <br /> | ||
<math>={t^2 \over4}-{t^2 \over2}</math> | <math>={t^2 \over4}-{t^2 \over2}</math> | ||
| Zeile 103: | Zeile 103: | ||
<math>-{t^2 \over4}</math> | <math>-{t^2 \over4}</math> | ||
| − | <math>TP(-{t \over2} | + | <math>TP \left(-{t \over2} ; -{t^2 \over4}\right)</math> |
<br /><br /> | <br /><br /> | ||
x-Koordinate nach t auflösen: | x-Koordinate nach t auflösen: | ||
| Zeile 117: | Zeile 117: | ||
<math>y=-{(-2x)^2 \over4}</math> | <math>y=-{(-2x)^2 \over4}</math> | ||
<br /> | <br /> | ||
| − | <math>=-{(-2x) | + | <math>=-{(-2x)\cdot(-2x) \over4}</math> |
<br /> | <br /> | ||
<math>=-{4x^2 \over4}</math> | <math>=-{4x^2 \over4}</math> | ||
Version vom 11. Dezember 2015, 10:16 Uhr
Die folgenden Kapitel werden anhand einer Aufgabe erklärt.
30px Aufgabe
Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte? |
Inhaltsverzeichnis |
Funktionenscharen
Berechnung der Extrempunkte:
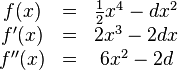
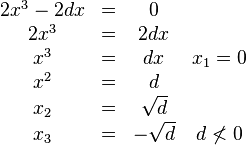
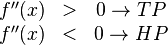
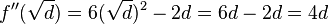
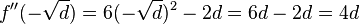
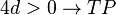für beide Extrempunkte
für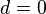 
liegt kein Tiefpunkt vor!
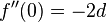
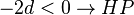, für 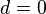liegt kein Hochpunkt vor!
Ortskurven
Allgemeine Herleitung einer Ortskurve
Hoch- bzw Tiefpunkt bestimmen
-> Die 1. Ableitung 0 setzen
-> Ergebnis in die 2. Ableitung einsetzen
-> Ergebnis größer 0 -> Tiefpunkt;
Ergebnis kleiner 0 -> Hochpunkt
Ortskurve bestimmen
-> x-Koordinate in die Funktion einsetzen -> Ergebnis bildet die y-Koordinate -> x-Koordinate nach t auflösen -> t Auflösung in y einsetzen -> Lösung = Ortskurvenfunktion
Probe mit Hilfe des GTRs
-> In "Y=" für y1,2,3 für t in der Funktion beliebige Zahlen einsetzen (z.B. 1,2 und 3) -> Ortskurvenfunktion in y4 einsetzen -> Im "Graph" überprüfen, ob die Ortskurve alle Funktionen an derselben Stelle durchläuft
Beispiel
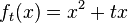
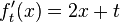
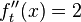
Hoch- bzw Tiefpunkt bestimmen:
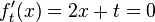
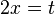
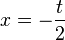
Kurvenverhalten:
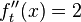
größer als 0 -> Tiefpunkt
Ortskurve bestimmen:
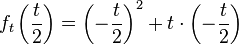
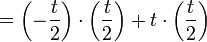
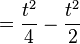
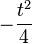
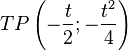
x-Koordinate nach t auflösen:
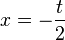
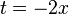
t Auflösung in y einsetzen:
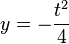
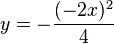
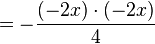
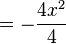
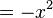--> Ortskurvenfunktion
Probe mit Hilfe des GTRs!
Bestimmung der Ortskurve der Hochpunkte:
Ortskurven sind Kurven, auf denen Punkte mit gleichen Eigenschaften einer Kurvenschar liegen z.B alle Hochpunkte.
Bestimmen von Ortskurven
Die Koordinaten des Extrempunktes sind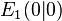 
, 
, 
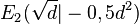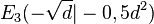
Koordinaten der Extrempunkte einzeln aufschreiben:
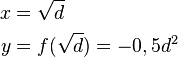
x - Koordinate nach Parameter auflösen:
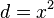
Diesen Parameter in die y - Gleichung einsetzen:
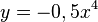
Gleichung der Ortskurve der Extrempunkte:
