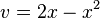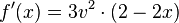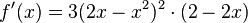Ableitungsregeln: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Quotientenregel)
 
(5 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 26: Zeile 26:
 
<math>f'(x)=a \cdot n \cdot x^{n-1}</math><br />
 
<math>f'(x)=a \cdot n \cdot x^{n-1}</math><br />
 
<br />
 
<br />
−
Bespiel:<br />
+
Beispiel:<br />
 
<br />
 
<br />
 
<math>f(x)=2x^3+4x^2+5x</math><br />
 
<math>f(x)=2x^3+4x^2+5x</math><br />
Zeile 46: Zeile 46:
 
<math>f(x)=(5x^2) \cdot x^{1 \over 2}</math><br />
 
<math>f(x)=(5x^2) \cdot x^{1 \over 2}</math><br />
 
<math>f'(x)=(10x) \cdot (x^{1 \over 2})+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}</math><br />
 
<math>f'(x)=(10x) \cdot (x^{1 \over 2})+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}</math><br />
−
<math>f'(x)=10x \cdot sqrt{x}+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}</math>
+
<math>f'(x)=10x \cdot \sqrt{x}+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}</math>
  
−
<span style="color: red">''Kann man das noch weiter umschreiben? [Btm]''</span>
 
  
 
=== Quotientenregel ===
 
=== Quotientenregel ===
Zeile 58: Zeile 57:
 
Kurzform: <br />
 
Kurzform: <br />
 
<math> f'= {{u' \cdot v- u \cdot v' } \over {v^2}} </math>
 
<math> f'= {{u' \cdot v- u \cdot v' } \over {v^2}} </math>
 +
<br />
  
−
Anwendungsbeispiel:
+
Anwendungsbeispiel:<br />
 
<math> f(x)= {{5 \cdot x^3 + 2 \cdot x^2} \over {x^2}} </math>
 
<math> f(x)= {{5 \cdot x^3 + 2 \cdot x^2} \over {x^2}} </math>
  
 
<math> f'= {{(15 \cdot x^2 + 4 \cdot x)\cdot x^2 }-{( 5 \cdot x^3 + 2 \cdot x^2) \cdot 2 \cdot x } \over {x^4}} </math>
 
<math> f'= {{(15 \cdot x^2 + 4 \cdot x)\cdot x^2 }-{( 5 \cdot x^3 + 2 \cdot x^2) \cdot 2 \cdot x } \over {x^4}} </math>
  
−
<math> f'= {{(15 \cdot x^2 + 4 \cdot x^3 ) - {( 10 \cdot x^4 + 4 \cdot x^3)} \over { x^4}} </math>
+
<math> f'= {{(15 \cdot x^2 + 4 \cdot x^3 )} - {( 10 \cdot x^4 + 4 \cdot x^3)} \over { x^4}} </math>
  
 
<math> f'= {{ 5\cdot x^4} \over {x^4}} </math>
 
<math> f'= {{ 5\cdot x^4} \over {x^4}} </math>
  
−
<math> f'={{ 5 \cdot x^4} \cdot {1 \over {x^4}} = {5} </math>
+
<math> f'= {{ 5 \cdot x^4} \cdot {1 \over{x^4}}} = {5} </math>
  
 
Quotienten lösen mit Hilfe der Produktregel:
 
Quotienten lösen mit Hilfe der Produktregel:
Zeile 98: Zeile 98:
 
äußere Funktion: <math>u=v^3</math>
 
äußere Funktion: <math>u=v^3</math>
 
<br />
 
<br />
−
innere Funktion: <math>v=2x-2x^2</math><br />
+
innere Funktion: <math>v=2x-x^2</math><br />
 
<br />
 
<br />
 
<math>f'(x)=3v^2\cdot(2-2x)</math><br />
 
<math>f'(x)=3v^2\cdot(2-2x)</math><br />
 
<br />
 
<br />
 
<math>f'(x)=3(2x-x^2)^2\cdot(2-2x)</math><br />
 
<math>f'(x)=3(2x-x^2)^2\cdot(2-2x)</math><br />

Aktuelle Version vom 11. Dezember 2015, 10:16 Uhr

Inhaltsverzeichnis

Bekannte Ableitungsregeln aus Klasse 10

Potenzregel

Allgemeine Formel:

f(x)=x^n
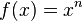
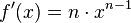
f'(x)=n \cdot x^{n-1}

Beispiel:

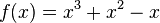
f(x)=x^3+x^2-x
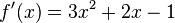
f'(x)=3x^2+2x-1

Summenregel

Allgemeine Formel:

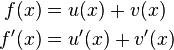
\begin{align} f(x)&=u(x)+v(x) \\ f'(x)&=u'(x) + v'(x) \end{align}

Faktorregel

Allgemeine Formel:

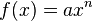
f(x)=ax^n
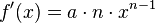
f'(x)=a \cdot n \cdot x^{n-1}

Beispiel:

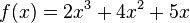
f(x)=2x^3+4x^2+5x
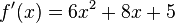
f'(x)=6x^2+8x+5

Neue Ableitungsregeln

Produktregel

Allgemeine Formel:

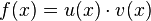
f(x)=u(x) \cdot v(x)

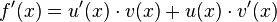
f'(x)=u'(x)\cdot v(x)+u(x)\cdot v'(x)

Kurzform: 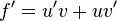f'=u'v+uv'


Rechenbeispiel:
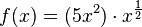
f(x)=(5x^2) \cdot x^{1 \over 2}
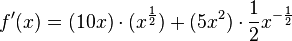
f'(x)=(10x) \cdot (x^{1 \over 2})+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}
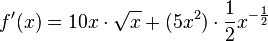
f'(x)=10x \cdot \sqrt{x}+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}


Quotientenregel

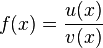
f(x)= {u(x)\over v(x)}
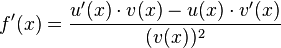
f'(x)= {{u'(x) \cdot v(x)- u(x) \cdot v'(x)} \over (v(x))^2}

Kurzform:
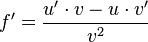
f'= {{u' \cdot v- u \cdot v' } \over {v^2}}

Anwendungsbeispiel:
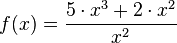
f(x)= {{5 \cdot x^3 + 2 \cdot x^2} \over {x^2}}

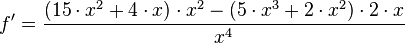
f'= {{(15 \cdot x^2 + 4 \cdot x)\cdot x^2 }-{( 5 \cdot x^3 + 2 \cdot x^2) \cdot 2 \cdot x } \over {x^4}}

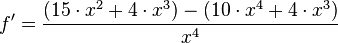
f'= {{(15 \cdot x^2 + 4 \cdot x^3 )} - {( 10 \cdot x^4 + 4 \cdot x^3)} \over { x^4}}

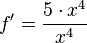
f'= {{ 5\cdot x^4} \over {x^4}}

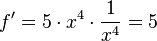
f'= {{ 5 \cdot x^4} \cdot {1 \over{x^4}}} = {5}

Quotienten lösen mit Hilfe der Produktregel: Trick: Quotienten in ein Produkt umschreiben und dann die Produktregel anwenden

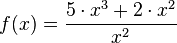
f(x)= {{5 \cdot x^3 + 2 \cdot x^2} \over {x^2}}

als Produkt: 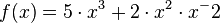f(x)= {{5 \cdot x^3 + 2 \cdot x^2} \cdot {x^-2}}

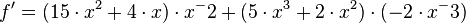
f'= {{(15 \cdot x^2 + 4 \cdot x) \cdot x^-2 + {( 5 \cdot x^3 + 2 \cdot x^2)} \cdot (-2 \cdot x^-3)}}

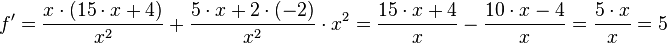
f'= {{x \cdot( 15 \cdot x +4 ) \over x^2} + {5 \cdot x + 2 \cdot (-2) \over x^2 } \cdot {x^2}} = {{15 \cdot x +4 \over x} - { 10 \cdot x - 4 \over x}} = {{ 5 \cdot x \over x }} = {5}

Kettenregel

Allgemeine Formel der Kettenregel:

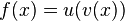
f(x)=u(v(x))

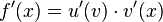
f'(x)=u'(v) \cdot v'(x)

Die Ableitung einer verketteten Funktion ist die Ableitung
der äußeren Funktion mal der Ableitung der inneren Funktion.

Beispiel:

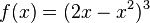
f(x)=(2x-x^2)^3

äußere Funktion: 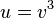u=v^3
innere Funktion: v=2x-x^2

f'(x)=3v^2\cdot(2-2x)

f'(x)=3(2x-x^2)^2\cdot(2-2x)

Von „http://fsg.zum.de/index.php?title=Ableitungsregeln&oldid=1638“