Kurvendiskussion: Unterschied zwischen den Versionen
(→Kriterien für Extremstellen) |
(→Kriterien für Extremstellen) |
||
| (13 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
===Kriterien=== | ===Kriterien=== | ||
| − | # notwendige Bedingung: <math>f'(x)=0 </math> <br /> ''Begründung: Die Ableitung(Steigung) am Extrempunkt ist 0 '' | + | # notwendige Bedingung: <math>f'(x)=0 </math> <br /> ''Begründung: Die Ableitung (Steigung) am Extrempunkt ist 0 '' |
# hinreichende Bedingung: | # hinreichende Bedingung: | ||
| − | ## schwache Bedingung: <math>f''( | + | ## schwache Bedingung: <math>f''(x_E)\not=0 </math> <br /> ''Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. |
| − | ## starke Bedingung: Vorzeichenwechsel | + | ## starke Bedingung: Vorzeichenwechsel von f '(x) an der Stelle des eventuellen Extrempunktes. <br /> ''Begründung: Die erste Ableitung muss ein Vorzeichenwechsel haben, da sonst ein Sattelpunkt vorliegt. |
| + | |||
| + | ===Beispiel=== | ||
| + | Bestimme die Extremstellen der Funktion | ||
| + | |||
| + | <math>f(x)=-\frac{1}{8}x^4-\frac{1}{3}x^3+1</math> <br /> | ||
| + | |||
| + | <math>f'(x)=-\frac{1}{2}x^3-x^2</math> | ||
| + | |||
| + | '''notwendige Bedingung:''' <math>f'(x_0)=0</math> <br /> | ||
| + | |||
| + | <math>-\frac{1}{2}x^3-x^2=0 \quad |x^2 \quad ausklammern </math> <br /> | ||
| + | <math>x^2\cdot\left(- \frac{1}{2}x-1\right)=0</math> <br /> | ||
| + | <math>x_1=0 </math> <br /> | ||
| + | <math>x_2=-2</math> | ||
| + | |||
| + | '''hinreichende Bedingung:''' <br /> | ||
| + | '''schwache Bedingung:''' <math>f''(x)\not= 0 </math> <br /> | ||
| + | |||
| + | <math> f''(x)= -\frac{3}{2}x^2-2x </math> <br /> | ||
| + | |||
| + | Untersuchung für x=0: <br /> | ||
| + | <math> f''(0)=0 </math> → schwache Bedingung für <math>x_1= 0 \quad </math> nicht erfüllt! <br /> | ||
| + | '''starke Bedingung:''' | ||
| + | <math>f'(1)=(-1)^2\cdot\left(-\frac{1}{2}\cdot1-1\right)=-\frac{1}{2} </math> <br /> | ||
| + | |||
| + | <math>f'(-1)=1^2\cdot\left(-\frac{1}{2}\cdot1-1\right)=-\frac{1}{2} </math> <br /> | ||
| + | → kein Vorzeichenwechsel also kein Extrema! <br /> | ||
| + | |||
| + | Untersuchung für <math>x=(-2)</math>: <br /> | ||
| + | <math>f''(-2)=-2<0</math> <br /> | ||
| + | → '''Hochpunkt''' bei <math>H(-2;f(-2))</math> <br /> | ||
| + | |||
| + | |||
| + | |||
| + | ===Aufgabe=== | ||
| + | Bestimme die Extremstellen der Funktion <math>f(x)=x^4-11</math> <br /> | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | <math>f'(x)=4x^3</math> <br /> | ||
| + | <math>f'(x_0)=0</math> <br \> | ||
| + | <math>x_1=0</math> <br \> | ||
| + | |||
| + | <math>f''(x)=12x^2</math> <br /> | ||
| + | '''schwache Bedingung:''' <br \> | ||
| + | <math> f''(0)=0 </math> → schwache Bedingung für <math>x_1= 0 \quad </math> nicht erfüllt! <br /> | ||
| + | |||
| + | '''starke Bedingung:''' | ||
| + | <math>f'(-1)=-4</math> <br /> | ||
| + | |||
| + | <math>f'(1)=4 </math> <br /> | ||
| + | → Vorzeichenwechsel an der Stelle x=0 <br \> | ||
| + | → '''Tiefpunkt'''(da Vorzeichenwechsel von - nach +) <br \> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </popup> | ||
== Kriterien für Wendestellen == | == Kriterien für Wendestellen == | ||
| + | '''Was ist eine Wendestelle?''' | ||
| + | |||
| + | Eine Wendestelle beschreibt einen Punkt im Graphen, an dem sich der Verlauf der Kurve ändert. Die Kurve einer Funktion kann entweder nach links oder nach rechts gekrümmt sein. Diesen Punkt kann man anhand der Ableitungen der Ausgangsfunktion finden. Für eine Wendestelle gibt es zwei Kriterien: | ||
| + | |||
| + | [[File:Inflection point.png|Inflection Point|rahmenlos]] | ||
| + | |||
| + | * '''Notwendiges Kriterium''' | ||
| + | |||
| + | Das notwendige Kriterium wird überprüft, um Stellen herauszufinden, an denen eine Wendestelle vorkommen kann. Dazu bildet man die zweite Ableitung und setzt diese mit Null gleich. Gibt es keine Nullstellen der zweiten Ableitung, so sind alle Wendestellen für die Ausgangsfunktion ausgeschlossen. An Extrema der zweiten Ableitung (<math>f''(x)=0</math>) können aber müssen nicht Wendestellen vorkommen. Um für Gewissheit zu sorgen muss man letztendlich die gefundenen Nullstellen mit dem hinreichenden Kriterium überprüfen. | ||
| + | |||
| + | |||
| + | * '''Hinreichendes Kriterium''' | ||
| + | |||
| + | Das hinreichende Kriterium dient zur Bestätigung einer Wendestelle und beschreibt gleichzeitig deren Verlauf (Links-Rechts-Kurve oder Rechts-Links-Kurve). Dazu bildet man die dritte Ableitung <math>f'''(x_w)</math> der Ausgangsfunktion <math>f(x)</math> und setzt diese gleich mit Null. Ist die dritte Ableitung der zu prüfenden Stelle ungleich 0, so entspricht diese einer Wendestelle. Das Ergebnis dieser Rechnung kann jedoch noch mehr aussagen: Ist der Wert kleiner als 0, so ist diese eine Links-Rechts-Wendestelle. Ist der Wert größer als 0, so entspricht diese einer Rechts-Links-Wendestelle. | ||
| + | |||
| + | |||
| + | ''Fazit für das hinreichende Kriterium'' | ||
| + | |||
| + | |||
| + | <math>f''' \neq 0</math>, wenn <math>f'''<0</math> dann Rechtskurve, wenn <math>f'''>0</math> dann Linkskurve | ||
| + | |||
| + | |||
| + | * '''Beispiel''' | ||
| + | |||
| + | Folgende Bedingungen müssen also erfüllt sein: | ||
| + | |||
| + | <math>f'(x)=0</math> | ||
| + | |||
| + | <math>f''(x)\not=0</math> | ||
| + | |||
| + | |||
| + | |||
| + | Wenn <math>f'''(x)>0</math>, dann ist bei <math>x</math> eine Rechts-Links-Wendestelle und wenn <math>f'''(x)<0</math>, dann ist x eine Links-Rechts-Wendestelle. | ||
| + | |||
| + | |||
| + | |||
| + | <math>f(x)={1\over9}x^3-{1\over3}x^2-{8\over3}x+{26\over9}</math> | ||
| + | |||
| + | |||
| + | Wir benötigen die erste Ableitung, um die zweite zu bilden: | ||
| + | |||
| + | |||
| + | <math>f'(x)={3\over9}x^2-{2\over3}x-{8\over3}</math> | ||
| + | |||
| + | |||
| + | Wir bilden die zweite Ableitung: | ||
| + | |||
| + | |||
| + | <math>f''(x)={2\over3}x-{2\over3}</math> | ||
| + | |||
| + | |||
| + | Wir setzen die zweite Ableitung gleich Null: | ||
| + | |||
| + | |||
| + | <math>f''(x)=0</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <math>{2\over3}x-{2\over3}=0</math> <math>\quad</math> <math>|+{2\over3}</math> | ||
| + | |||
| + | <math>{2\over3}x={2\over3}</math> <math>\quad</math> <math>|\cdot{3\over2}</math> | ||
| + | |||
| + | <math>x=1</math> | ||
| + | |||
| + | |||
| + | Bei <math>x=1</math> befindet sich unsere Wendestelle. Wir setzen diesen x-Wert in unsere Funktion ein, um den y-Wert zu bekommen: | ||
| + | |||
| + | |||
| + | <math>f(1)={1\over9}\cdot1^3-{1\over3}\cdot1^2-{8\over3}\cdot1+{26\over9}=0\rightarrow W(1|0)</math> | ||
| + | |||
| + | |||
| + | Unser Wendpunkt ist folglich <math>W(1|0)</math>. Noch schnell die dritte Ableitung überprüfen, dass die auch nicht Null wird: | ||
| + | |||
| + | |||
| + | <math>f'''(x)={2\over3}>0\rightarrow Rechts-Links-Wendepunkt</math> | ||
== vollständige Kurvendiskussion == | == vollständige Kurvendiskussion == | ||
| + | |||
| + | === Definitionsbereich === | ||
| + | Mit dem Definitionsbereich sind alle Zahlen für x gemeint, die man in die Funktion einsetzen kann.<br /> | ||
| + | |||
| + | === Symmetrie === | ||
| + | * Achsensymmetrie zur y-Achse: <math>f(-x)=f(x)</math> | ||
| + | * Punktsymmetrie zum Ursprung: <math>f(-x)=-f(x)</math> | ||
| + | Sind in der Funktion nur gerade Exponenten vorhanden, kann die Funktion nur achsensymmetrisch sein. | ||
| + | Sind jedoch nur ungerade Exponenten vorhanden, so kann sie nur punktsymmetrisch sein. | ||
| + | |||
| + | === Verschiebung === | ||
| + | * um ''c'' in x-Richtung <math>y=f(x-c)</math> Für ''c > 0'' nach links verschoben, für ''c < 0'' nach rechts. | ||
| + | * um ''d'' in y-Richtung <math>y=f(x)+d</math> Für ''d > 0'' nach oben verschoben, für ''d < 0'' nach unten. | ||
| + | |||
| + | === Schnittstellen mit den Achsen === | ||
| + | Man setzt die Funktion mit Null gleich und löst die Gleichung nach ''x'' auf. Daraus erhält man die Schnittstellen mit der x-Achse (Nullstellen).<br /> | ||
| + | Um die Schnittstelle mit der y-Achse auszurechnen, setzt man für ''x'' in der Funktion Null ein und rechnet die Gleichung aus. | ||
| + | |||
| + | === Monotonie === | ||
| + | <math>f'(x)>0</math> => f streng monoton wachsend | ||
| + | <math>f'(x)<0</math> => f streng monoton fallend | ||
| + | |||
| + | <math>f'(x)\ge0</math> => f monoton wachsend | ||
| + | <math>f'(x)\le0</math> => f monoton fallend | ||
| + | |||
| + | === Globalverlauf === | ||
| + | * Globalverlauf für gerade Funktionen (nur gerade Exponenten): | ||
| + | <math>x\to\infty</math> => <math>y\to\infty</math> Gesprochen: Für ''x'' gegen unendlich, läuft ''y'' gegen unendlich<br /> | ||
| + | <math>x\to-\infty</math> => <math>y\to\infty</math> Gesprochen: Für ''x'' gegen minus unendlich, läuft ''y'' gegen unendlich | ||
| + | * Globalverlauf für ungerade Funktionen (nur ungerade Exponenten): | ||
| + | <math>x\to\infty</math> => <math>y\to\infty</math> Gesprochen: Für ''x'' gegen unendlich, läuft ''y'' gegen unendlich<br /> | ||
| + | <math>x\to-\infty</math> => <math>y\to-\infty</math> Gesprochen: Für ''x'' gegen minus unendlich, läuft ''y'' gegen minus unendlich | ||
| + | '''! Anmerkung: Eine negative Basis spiegelt die Kurven an der x-Achse, wodurch auch die Globalverläufe "gespiegelt" werden.''' | ||
| + | |||
| + | === Beispielaufgabe === | ||
| + | Führe ein vollständige Kurvendiskussion an dieser Funktion durch: <math>f(x) = \frac{1}{4}x^4 - 2x^2 - \frac{9}{4}</math> | ||
| + | |||
| + | <popup name="Lösungen"> | ||
| + | * Definitionsbereich: Alle reellen Zahlen | ||
| + | * Symmetrie: Achsensymmetrisch, da nur gerade Exponenten und keine Verschiebung auf der x-Achse vorhanden ist. | ||
| + | * Nullstellen (Schnittstellen mit der x-Achse): <math>x_1 = 3</math> und <math>x_2 = -3</math> | ||
| + | * Schnittstelle mit der y-Achse (für x Null einsetzen): <math>f(0) = \frac{1}{4} \cdot 0^2 - 2\cdot0^2 - \frac{9}{4} = -\frac{9}{4}</math> | ||
| + | * Monotonie: | ||
| + | <math>(\infty; -2]</math> streng monoton fallend | ||
| + | <math>[-2; 0]</math> streng monoton steigend | ||
| + | <math>[0; 2]</math> streng monoton fallend | ||
| + | <math>[2; \infty]</math> streng monoton steigend | ||
| + | * Globalverlauf: | ||
| + | <math>x\to\infty</math> => <math>y\to\infty</math> Gesprochen: Für ''x'' gegen unendlich, läuft ''y'' gegen unendlich<br /> | ||
| + | <math>x\to-\infty</math> => <math>y\to\infty</math> Gesprochen: Für ''x'' gegen minus unendlich, läuft ''y'' gegen unendlich | ||
| + | </popup> | ||
Aktuelle Version vom 11. Dezember 2015, 10:55 Uhr
Inhaltsverzeichnis |
Kriterien für Extremstellen
Definition
Ein Hochpunkt hat den größten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von positiv (+) nach negativ (-) .
Ein Tiefpunkt hat den kleinsten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von negativ (-) nach positiv (+) .
Kriterien
- notwendige Bedingung:
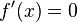
Begründung: Die Ableitung (Steigung) am Extrempunkt ist 0 - hinreichende Bedingung:
- schwache Bedingung:
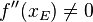
Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. - starke Bedingung: Vorzeichenwechsel von f '(x) an der Stelle des eventuellen Extrempunktes.
Begründung: Die erste Ableitung muss ein Vorzeichenwechsel haben, da sonst ein Sattelpunkt vorliegt.
- schwache Bedingung:
Beispiel
Bestimme die Extremstellen der Funktion
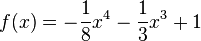
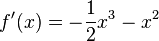
notwendige Bedingung: 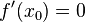
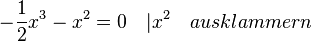
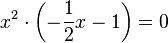
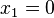
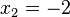
hinreichende Bedingung:
schwache Bedingung: 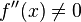
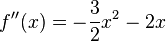
Untersuchung für x=0:
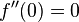 → schwache Bedingung für
→ schwache Bedingung für 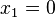 nicht erfüllt!
nicht erfüllt!
starke Bedingung:
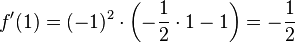
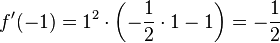
→ kein Vorzeichenwechsel also kein Extrema!
Untersuchung für 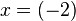 :
:
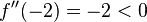
→ Hochpunkt bei 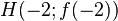
Aufgabe
Bestimme die Extremstellen der Funktion 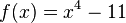
Kriterien für Wendestellen
Was ist eine Wendestelle?
Eine Wendestelle beschreibt einen Punkt im Graphen, an dem sich der Verlauf der Kurve ändert. Die Kurve einer Funktion kann entweder nach links oder nach rechts gekrümmt sein. Diesen Punkt kann man anhand der Ableitungen der Ausgangsfunktion finden. Für eine Wendestelle gibt es zwei Kriterien:
- Notwendiges Kriterium
Das notwendige Kriterium wird überprüft, um Stellen herauszufinden, an denen eine Wendestelle vorkommen kann. Dazu bildet man die zweite Ableitung und setzt diese mit Null gleich. Gibt es keine Nullstellen der zweiten Ableitung, so sind alle Wendestellen für die Ausgangsfunktion ausgeschlossen. An Extrema der zweiten Ableitung (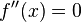 ) können aber müssen nicht Wendestellen vorkommen. Um für Gewissheit zu sorgen muss man letztendlich die gefundenen Nullstellen mit dem hinreichenden Kriterium überprüfen.
) können aber müssen nicht Wendestellen vorkommen. Um für Gewissheit zu sorgen muss man letztendlich die gefundenen Nullstellen mit dem hinreichenden Kriterium überprüfen.
- Hinreichendes Kriterium
Das hinreichende Kriterium dient zur Bestätigung einer Wendestelle und beschreibt gleichzeitig deren Verlauf (Links-Rechts-Kurve oder Rechts-Links-Kurve). Dazu bildet man die dritte Ableitung 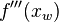 der Ausgangsfunktion
der Ausgangsfunktion  und setzt diese gleich mit Null. Ist die dritte Ableitung der zu prüfenden Stelle ungleich 0, so entspricht diese einer Wendestelle. Das Ergebnis dieser Rechnung kann jedoch noch mehr aussagen: Ist der Wert kleiner als 0, so ist diese eine Links-Rechts-Wendestelle. Ist der Wert größer als 0, so entspricht diese einer Rechts-Links-Wendestelle.
und setzt diese gleich mit Null. Ist die dritte Ableitung der zu prüfenden Stelle ungleich 0, so entspricht diese einer Wendestelle. Das Ergebnis dieser Rechnung kann jedoch noch mehr aussagen: Ist der Wert kleiner als 0, so ist diese eine Links-Rechts-Wendestelle. Ist der Wert größer als 0, so entspricht diese einer Rechts-Links-Wendestelle.
Fazit für das hinreichende Kriterium
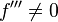 , wenn
, wenn 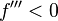 dann Rechtskurve, wenn
dann Rechtskurve, wenn 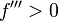 dann Linkskurve
dann Linkskurve
- Beispiel
Folgende Bedingungen müssen also erfüllt sein:
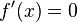
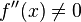
Wenn 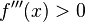 , dann ist bei
, dann ist bei 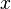 eine Rechts-Links-Wendestelle und wenn
eine Rechts-Links-Wendestelle und wenn 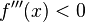 , dann ist x eine Links-Rechts-Wendestelle.
, dann ist x eine Links-Rechts-Wendestelle.
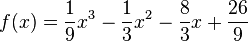
Wir benötigen die erste Ableitung, um die zweite zu bilden:
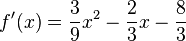
Wir bilden die zweite Ableitung:
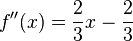
Wir setzen die zweite Ableitung gleich Null:
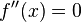
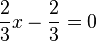


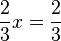

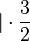
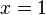
Bei 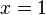 befindet sich unsere Wendestelle. Wir setzen diesen x-Wert in unsere Funktion ein, um den y-Wert zu bekommen:
befindet sich unsere Wendestelle. Wir setzen diesen x-Wert in unsere Funktion ein, um den y-Wert zu bekommen:
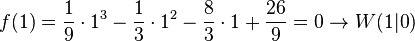
Unser Wendpunkt ist folglich 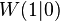 . Noch schnell die dritte Ableitung überprüfen, dass die auch nicht Null wird:
. Noch schnell die dritte Ableitung überprüfen, dass die auch nicht Null wird:
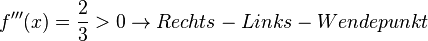
vollständige Kurvendiskussion
Definitionsbereich
Mit dem Definitionsbereich sind alle Zahlen für x gemeint, die man in die Funktion einsetzen kann.
Symmetrie
- Achsensymmetrie zur y-Achse:
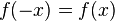
- Punktsymmetrie zum Ursprung:
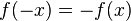
Sind in der Funktion nur gerade Exponenten vorhanden, kann die Funktion nur achsensymmetrisch sein. Sind jedoch nur ungerade Exponenten vorhanden, so kann sie nur punktsymmetrisch sein.
Verschiebung
- um c in x-Richtung
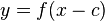 Für c > 0 nach links verschoben, für c < 0 nach rechts.
Für c > 0 nach links verschoben, für c < 0 nach rechts.
- um d in y-Richtung
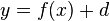 Für d > 0 nach oben verschoben, für d < 0 nach unten.
Für d > 0 nach oben verschoben, für d < 0 nach unten.
Schnittstellen mit den Achsen
Man setzt die Funktion mit Null gleich und löst die Gleichung nach x auf. Daraus erhält man die Schnittstellen mit der x-Achse (Nullstellen).
Um die Schnittstelle mit der y-Achse auszurechnen, setzt man für x in der Funktion Null ein und rechnet die Gleichung aus.
Monotonie
=> f streng monoton wachsend
=> f streng monoton fallend
=> f monoton wachsend
=> f monoton fallend
Globalverlauf
- Globalverlauf für gerade Funktionen (nur gerade Exponenten):
=>
Gesprochen: Für x gegen unendlich, läuft y gegen unendlich
=>
Gesprochen: Für x gegen minus unendlich, läuft y gegen unendlich
- Globalverlauf für ungerade Funktionen (nur ungerade Exponenten):
=>
Gesprochen: Für x gegen unendlich, läuft y gegen unendlich
=>
Gesprochen: Für x gegen minus unendlich, läuft y gegen minus unendlich
! Anmerkung: Eine negative Basis spiegelt die Kurven an der x-Achse, wodurch auch die Globalverläufe "gespiegelt" werden.
Beispielaufgabe
Führe ein vollständige Kurvendiskussion an dieser Funktion durch: 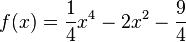
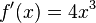
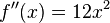
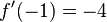
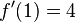
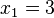 und
und 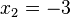
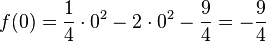
![(\infty; -2]](/images/math/0/9/c/09ca05af5f39812d881a259cd7a0f1cd.png) streng monoton fallend
streng monoton fallend
![[-2; 0]](/images/math/7/f/5/7f5e70e9a81ee7bf87ee7b5f1b55ec53.png) streng monoton steigend
streng monoton steigend
![[0; 2]](/images/math/7/a/6/7a6df794fbd855c933275991bed807e4.png) streng monoton fallend
streng monoton fallend
![[2; \infty]](/images/math/8/1/1/811448d5eb50e1c634d30500e1835308.png) streng monoton steigend
streng monoton steigend

