Beschränktes Wachstum: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.<br />
 
Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.<br />
−
Wie das exponentielle Wachstum kann auch das beschränkte Wachstum mit und ohne <math>{e}</math> gebildet werden.
 
  
−
==Funktionsterm ohne e==
+
==Funktionsterm==
−
Der allgemeine Funktionsterm des beschränkten Wachstums ohne <math>{e}</math> lautet:<br />
+
−
<math>{f(x)=S-a \cdot b^{-x}}</math><br />
+
−
<math>{S}</math> steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.<br />
+
−
<math>{a}</math> ergibt addiert (nachunten begrenzt) beziehungsweise subtrahiert (nach oben begrenzt) mit/von <math>{S}</math> den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{x=0}</math>. Zudem bestimmt das Vorzeichen vor dem <math>{a}</math>, ob das Wachstum nach oben oder nach unten begrenzt ist.<br />
+
−
<math>{b}</math> ist der Wachstums- eziehungsweise Zerfallsfaktor um den <math>{a}</math> in einem bestimmten Zeitraum multipliziert wird.<br />
+
−
 
+
−
===Beispiel===
+
−
Ein Heißgetränk hat eine Temperatur von 50 °C und kühlt auf die Umgebungstemperatur von 20 °C ab
+
−
 
+
−
==Funktionsterm mit e==
+
 
<math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br />
 
<math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br />
 
<math>{S}</math>  steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.<br />
 
<math>{S}</math>  steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.<br />
Zeile 20: Zeile 9:
 
[[Datei:Be Wachstum2.png|rahmenlos|ohne]]<br />
 
[[Datei:Be Wachstum2.png|rahmenlos|ohne]]<br />
  
−
===Differenzialgleichung===
+
==Anfangsbestand berechnen==
−
Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums<br />
+
Um den Anfangsbestand zu berechnen, muss der restliche Funktionsterm auf <math>{a}</math> umgeformt werden.<br />
−
<math>{f'(x)=k \cdot (S-f(x))}</math>.<br /><br />
+
<math> \begin{align}
−
Erklärung:<br />
+
y &= S-a \cdot e^{-k \cdot x} |-S \\
−
Die Ableitund des Funktionsterms lautet: <br />
+
y-S &= -a \cdot e^{-k \cdot x} |: e^{-k \cdot S} \\
−
<math>{f'(x)=k \cdot a \cdot e^{-k \cdot x}}</math><br />
+
\frac{y-S}{e^{-k \cdot x}} &= -a | \cdot -1 \\
−
Um daraus eine Differenzialgleichung zu machen, muss neben <math>{f'(x)}</math> auch <math>{f(x)}</math> in der Funktion enthalten sein. Dafür muss diese zuerst umgeformt werden:<br />
+
-\frac{y-S}{e^{-k \cdot x}} &= a \\
−
<math>{f'(x)=k(a \cdot e^{-k \cdot x})}</math><br />
+
-(y-S) \cdot e^{k \cdot x} &= a
−
Jetzt fehlt nur noch die Schranke <math>{S}</math>:<br />
+
\end{align} </math>
−
<math>{f'(x)=k(S-({\color{red}S-a \cdot e^{-k \cdot x}}))}</math><br />
+
−
Der markierte Teil ist identisch mit <math>{f(x)}</math> und kann daher ersetzt werden:<br />
+
−
<math>{f'(x)=k(S-{\color{red}f(x)})}</math><br />
+
  
−
==Beispiel==
+
===Beispiel===
−
[[Datei:BeWachstum3.png|rahmenlos|rechts]]
+
Gegeben ist die Gleichung <br />
−
Nach dem Einpflanzen wächst ein Baum recht schnell, jedoch wächst er langsamer je größer er wird, sodass sich seine Höhe einer natürlichen Grenze annähert. Diese Höhe (in Metern) kann mit der Funktion<br />
+
<math>{49,5=50-a \cdot e^{-0,75 \cdot 6}}</math><br /><br />
−
<math>{15-15 \cdot e^{-0,5 \cdot x}}</math> <br />
+
Um den Anfangsbestand zu berechnen müssen die Werte in die umgeformte Gleichung eingesetzt werden.<br />
−
(x in Jahren) beschrieben werden.
+
<math> \begin{align}
−
<br /><br /><br />
+
a &=-(49,5-50) \cdot e^{0,75 \cdot 6} \\
 +
a & \approx 45
 +
\end{align} </math><br /><br />
  
−
==Aufgaben==
+
{{Aufgabe|Gegeben ist die Gleichung <br />
−
{{Aufgabe|Bei Beobachtungsbeginn bedeckt eine Algenart 5 Quadratkilometer des Grundes eines Sees. Die Algen breiten sich innerhalb des 90 Quadratmeter großen Sees aus. Die von den Algen bedeckte Fläche kann mit der Funktion<br /><br />
+
<math>{52,15 = 60-58 \cdot e^{-0,4 \cdot 5}}</math><br />
−
<math>{90-85 \cdot e^{-0,1 \cdot x}}</math><br /><br />
+
Berechnen Sie <math>{a}</math><br />
−
(x in Monaten) beschrieben werden.
+
−
1) Geben Sie den Funktionsterm als Differenzialsgleichung an!
+
 
<popup name="Lösung">
 
<popup name="Lösung">
−
<math>{f'(x)=0,1(90-f(x))}</math>
+
<math> \begin{align}
 +
a &= -(52,15-60) \cdot e^{0,4 \cdot 5} \\
 +
a & \approx 58
 +
\end{align} </math>
 
</popup>
 
</popup>
−
2) Welche Fläche bedecken die Algen nach zweieinhalb Jahren?
+
}}
−
<popup name="Lösung">
+
 
−
<math>{f(30)=90-85 \cdot e^{-0,1 \cdot 30}}</math><br />
+
==Wachstumsgeschwindigkeit berechnen==
−
<math>{f(30) \approx 85,77}</math><br />
+
Um die wachstumsgeschwindigkeit zu berechnen, muss die Ableitung gebildet werden.<br />
−
Nach zweieinhalb Jahren haben die Algen ungefähr 85,77 Quadratmeter des Seegrundes bedeckt.
+
<math> \begin{align}
−
</popup>
+
f(x) &= S-a \cdot e^{-k \cdot x} \\
−
3) Wann bedecken die Algen eine Fläche von 75 Quadratkilometern?
+
f'(x) &= k(S-(S-a \cdot e^{-k \cdot x})) \\
 +
f'(X) &= k \cdot a \cdot e^{-k \cdot x}
 +
\end{align} </math>
 +
 
 +
===Beispiel===
 +
Gegeben ist die Funktionsgleichung <br />
 +
<math>{f(x)=100-99 \cdot e^{-1,2 \cdot x}}</math> <br />
 +
Also lautet die Ableitungsfunktion<br />
 +
<math>{f'(x)= 1,2 \cdot 99 \cdot e^{-1,2 \cdot x}}</math><br />
 +
Damit lässt sich die Wachststumsgeschwindigkeit der Ausgangsgleichung an jeder beliebigen Stelle berechnen.<br /><br />
 +
 
 +
{{Aufgabe|Gegeben ist die Funktionsgleichung <br />
 +
<math>{f(x)= 122-117 \cdot e^{-0,15 cdot x}}</math><br />
 +
Geben Sie die Wachstumsgeschwindigkeit an der Stelle <math>{x=9}</math> an!<br />
 
<popup name="Lösung">
 
<popup name="Lösung">
 
<math> \begin{align}
 
<math> \begin{align}
−
75 &=90-85 \cdot e^{-0,1 \cdot x}|-90 \\
+
f'(x) &=0,15 \cdot 117 \cdot e^{-0,15 \cdot x} \\
−
-15 &=-85 \cdot e^{-01 \cdot x}|:-85 \\
+
f'(9) &=0,15 \cdot 117 \cdot e^{-0,15 \cdot 9} \\
−
\tfrac{15}{85} &=e^{-0,1 \cdot x}|ln \\
+
f'(9) & \approx 4,55
−
ln(\tfrac{15}{85}) &=-0,1 \cdot x| \cdot -10 \\
+
\end{align} </math>
−
-10 \cdot ln(\tfrac{15}{85}) &=x \\
+
−
17,35 & \approx x
+
−
\end{align} </math><br />
+
−
Nach ungefähr 17,35 Monaten bedecken die Algen 75 Quadratkilometer des Seegrundes.
+
 
</popup>
 
</popup>
 
}}
 
}}

Version vom 4. Oktober 2018, 15:05 Uhr

Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.

Inhaltsverzeichnis

Funktionsterm

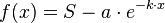
{f(x)=S-a \cdot e^{-k \cdot x}}

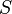{S} steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.
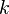{k} steht für die Wachstumskonstante.
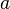{a} steht für den Anfangsbestand, also den Bestand zum Zeitpunkt 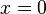{x=0} . Zudem bestimmt das Vorzeichen vor dem 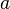{a}, ob das Wachstum nach oben oder nach unten begrenzt ist.

BeWachstum1.png
Be Wachstum2.png

Anfangsbestand berechnen

Um den Anfangsbestand zu berechnen, muss der restliche Funktionsterm auf 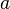{a} umgeformt werden.
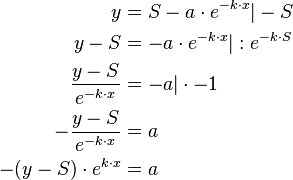
\begin{align} y &= S-a \cdot e^{-k \cdot x} |-S \\ y-S &= -a \cdot e^{-k \cdot x} |: e^{-k \cdot S} \\ \frac{y-S}{e^{-k \cdot x}} &= -a | \cdot -1 \\ -\frac{y-S}{e^{-k \cdot x}} &= a \\ -(y-S) \cdot e^{k \cdot x} &= a \end{align}

Beispiel

Gegeben ist die Gleichung
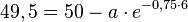
{49,5=50-a \cdot e^{-0,75 \cdot 6}}

Um den Anfangsbestand zu berechnen müssen die Werte in die umgeformte Gleichung eingesetzt werden.
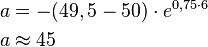
\begin{align} a &=-(49,5-50) \cdot e^{0,75 \cdot 6} \\ a & \approx 45 \end{align}

30px   Aufgabe

Gegeben ist die Gleichung
{52,15 = 60-58 \cdot e^{-0,4 \cdot 5}}
Berechnen Sie {a}

Wachstumsgeschwindigkeit berechnen

Um die wachstumsgeschwindigkeit zu berechnen, muss die Ableitung gebildet werden.
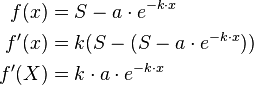
\begin{align} f(x) &= S-a \cdot e^{-k \cdot x} \\ f'(x) &= k(S-(S-a \cdot e^{-k \cdot x})) \\ f'(X) &= k \cdot a \cdot e^{-k \cdot x} \end{align}

Beispiel

Gegeben ist die Funktionsgleichung
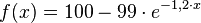
{f(x)=100-99 \cdot e^{-1,2 \cdot x}}
Also lautet die Ableitungsfunktion
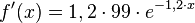
{f'(x)= 1,2 \cdot 99 \cdot e^{-1,2 \cdot x}}
Damit lässt sich die Wachststumsgeschwindigkeit der Ausgangsgleichung an jeder beliebigen Stelle berechnen.

30px   Aufgabe

Gegeben ist die Funktionsgleichung
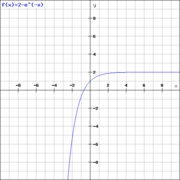
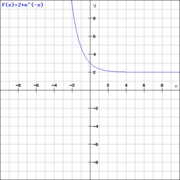
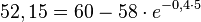
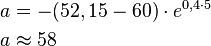
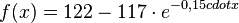
{f(x)= 122-117 \cdot e^{-0,15 cdot x}}
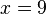Geben Sie die Wachstumsgeschwindigkeit an der Stelle {x=9} an!

Von „http://fsg.zum.de/index.php?title=Beschränktes_Wachstum&oldid=1821“