Rotationskörper: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Rotationskörper == Rotationskörper werden Körper genannt, welche durch Rotation einer erzeugenden Kurve um eine Achse entstehen. <br /> Die Achse um…“) |
|||
| Zeile 5: | Zeile 5: | ||
=== Wozu braucht man Rotationskörper ===. | === Wozu braucht man Rotationskörper ===. | ||
| − | Mit Hilfe von Rotationskörpern kann man das Volumen eines #runden# Körpers bestimmen, beispielsweise | + | Mit Hilfe von Rotationskörpern kann man das Volumen eines #runden# Körpers bestimmen, beispielsweise von einem Glas. |
=== Herleitung des Volumens von Rotationskörpern === | === Herleitung des Volumens von Rotationskörpern === | ||
| − | Ein Rotationskörper entsteht aus der Rotation einer Rotationsfläche um eine Rotationsachse. Die Rotationsfläche entspricht hierbei der Fläche unter dem Graphen der erzeugenden Funktion <math>f</math> im Intervall <math>[a;b]</math>. Ähnlich wie auch bei der Herleitung der | + | Ein Rotationskörper entsteht aus der Rotation einer Rotationsfläche um eine Rotationsachse. Die Rotationsfläche entspricht hierbei der Fläche unter dem Graphen der erzeugenden Funktion <math>f</math> im Intervall <math>[a;b]</math>. Ähnlich wie auch bei der Herleitung der Fläche unter Kurven (Integrale) nähern wir diese Fläche mit Rechtecken der Breite <math>h</math> an. Der Grenzwert dieser Fläche für immer schmalere Rechtecke, d.h. h→0 entspricht dem Integral <math>\int_{a}^{b}f(x)dx</math> <br />. |
| − | + | Bei Rotaionskörpern wird ähnlich vorgegangen. Statt Rechtecken mit Breite <math>h</math> verwendet man Zylinder mit Höhe <math>h</math> | |
- Vergehensweise ähnlich der Bestimmung mit Hilfe Integralen | - Vergehensweise ähnlich der Bestimmung mit Hilfe Integralen | ||
- | - | ||
- Annäherung des Rotationskörpers durch Zylinder mit Höhe h | - Annäherung des Rotationskörpers durch Zylinder mit Höhe h | ||
Version vom 3. November 2018, 16:16 Uhr
Rotationskörper
Rotationskörper werden Körper genannt, welche durch Rotation einer erzeugenden Kurve um eine Achse entstehen.
Die Achse um welche rotiert wird, bezeichnet man als Rotations- bzw. Figurenachse. Die von der Kurve eingeschlossene Fläche heißt Rotationsfläche.
Die Rotationsachse und die erzeugende Kurve müssen in der gleichen Ebene liegen.
=== Wozu braucht man Rotationskörper ===. Mit Hilfe von Rotationskörpern kann man das Volumen eines #runden# Körpers bestimmen, beispielsweise von einem Glas.
Herleitung des Volumens von Rotationskörpern
Ein Rotationskörper entsteht aus der Rotation einer Rotationsfläche um eine Rotationsachse. Die Rotationsfläche entspricht hierbei der Fläche unter dem Graphen der erzeugenden Funktion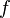 
im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png)
. Ähnlich wie auch bei der Herleitung der Fläche unter Kurven (Integrale) nähern wir diese Fläche mit Rechtecken der Breite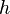 
an. Der Grenzwert dieser Fläche für immer schmalere Rechtecke, d.h. h→0 entspricht dem Integral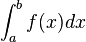 
.
Bei Rotaionskörpern wird ähnlich vorgegangen. Statt Rechtecken mit Breite 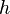verwendet man Zylinder mit Höhe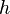
- Vergehensweise ähnlich der Bestimmung mit Hilfe Integralen - - Annäherung des Rotationskörpers durch Zylinder mit Höhe h
