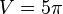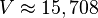Rotationskörper: Unterschied zwischen den Versionen
(→Rotationskörper um die y - Achse) |
|||
| Zeile 46: | Zeile 46: | ||
<math>V=\pi\int_{a}^{b}(g(y))^2dy</math> bestimmen <br /> | <math>V=\pi\int_{a}^{b}(g(y))^2dy</math> bestimmen <br /> | ||
Hier wird die Funktion um die y-Achse rotiert. | Hier wird die Funktion um die y-Achse rotiert. | ||
| − | + | Um das Volumen eines solchen Rotationskörpers zu bestimmen, wird dieser mithilfe der Umkehrfunktion so "gedreht", dass dieser um die x-Achse rotiert, dann kann das Volumen wie zuvor bei der <br> | |
| − | + | Rotation um die x-Achse beschrieben berechnet werden | |
| − | + | ||
==== Beispielrechnung ==== | ==== Beispielrechnung ==== | ||
Zur Berechnung des Volumens des Rotationskörpers der Funktion <math>g(x)=x^2</math> im Intervall von 0 bis 5. <br /> | Zur Berechnung des Volumens des Rotationskörpers der Funktion <math>g(x)=x^2</math> im Intervall von 0 bis 5. <br /> | ||
| Zeile 59: | Zeile 58: | ||
<p></p> | <p></p> | ||
<p></p> | <p></p> | ||
| − | ===== Berechnung des | + | ===== Berechnung des Volumens ===== |
<math>V=\pi \int_{0}^{25}(\sqrt{y})^2dy</math> | <math>V=\pi \int_{0}^{25}(\sqrt{y})^2dy</math> | ||
<p></p> | <p></p> | ||
| Zeile 74: | Zeile 73: | ||
<math>V \approx 981,75</math> | <math>V \approx 981,75</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==== Interaktive Volumensberechnung mit Rotationskörpern ==== | ==== Interaktive Volumensberechnung mit Rotationskörpern ==== | ||
Version vom 1. Dezember 2018, 13:37 Uhr
Inhaltsverzeichnis |
Rotationskörper
Rotationskörper werden Körper genannt, welche durch Rotation einer erzeugenden Kurve um eine Achse entstehen.
Die Achse um welche rotiert wird, bezeichnet man als Rotations- bzw. Figurenachse. Die von der Kurve eingeschlossene Fläche heißt Rotationsfläche.
Die Rotationsachse und die erzeugende Kurve müssen in der gleichen Ebene liegen.
[ www.geogebra.org is not an authorized iframe site ]
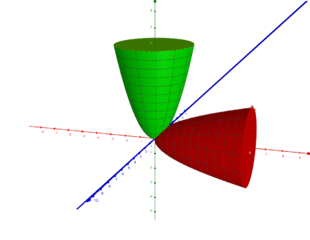
Rotationskörper der Funktion 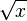 an der x- und der y-Achse.
an der x- und der y-Achse.
Wozu braucht man Rotationskörper
Mit Hilfe von Rotationskörpern kann man das Volumen eines runden Körpers bestimmen.
Herleitung des Volumens von Rotationskörpern um die x-Achse
Ein Rotationskörper entsteht aus der Rotation einer Rotationsfläche um eine Rotationsachse. Die Rotationsfläche entspricht hierbei der Fläche unter dem Graphen der erzeugenden Funktion 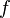 im Intervall
im Intervall ![[a;b]](/images/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) . Ähnlich wie auch bei der Herleitung der Fläche unter Kurven (Integrale) nähern wir diese Fläche mit Rechtecken der Breite
. Ähnlich wie auch bei der Herleitung der Fläche unter Kurven (Integrale) nähern wir diese Fläche mit Rechtecken der Breite 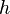 an. Der Grenzwert dieser Fläche für immer schmalere Rechtecke, d.h. h→0 entspricht dem Integral
an. Der Grenzwert dieser Fläche für immer schmalere Rechtecke, d.h. h→0 entspricht dem Integral 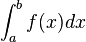 .
.
Bei Rotaionskörpern wird ähnlich vorgegangen. Statt Rechtecken mit Breite 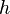 verwendet man Zylinder mit Höhe
verwendet man Zylinder mit Höhe 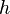 .
.
Für das Volumen eines Zylinders gilt: 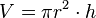 . Der Radius entspricht hierbei dem Funktionswert an der entsprechende Stelle. Damit gilt für das Volumen der Kreisscheibe an der Stelle
. Der Radius entspricht hierbei dem Funktionswert an der entsprechende Stelle. Damit gilt für das Volumen der Kreisscheibe an der Stelle 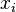 :
: 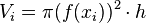 .
.
Auch hier erhält man für den Grenzfall h→0 den exakten Wert, in diesem Fall für das Volumen. Für dieses gilt:
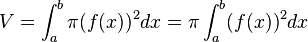 .
.
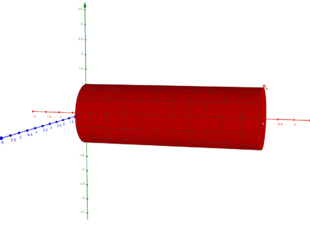
Rotationskörper um die x - Achse
Zur Berechnung des Volumens des Rotationskörpers der Funktion 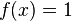 von 0 bis 5
von 0 bis 5
Der Flächeninhalt eines Rotationskörpers um die x - Achse lässt sich mithilfe der Formel
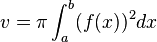 bestimmen.
bestimmen.
Als Beispiel soll hier die Funktion 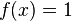 verwendet werden (siehe Abbildung).
verwendet werden (siehe Abbildung).
Beispielrechnung
Rotationskörper um die y - Achse
Der Flächeninhalt eines Rotationskörpers um die y - Achse lässt sich mithilfe der Formel
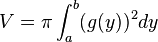 bestimmen
bestimmen
Hier wird die Funktion um die y-Achse rotiert.
Um das Volumen eines solchen Rotationskörpers zu bestimmen, wird dieser mithilfe der Umkehrfunktion so "gedreht", dass dieser um die x-Achse rotiert, dann kann das Volumen wie zuvor bei der
Rotation um die x-Achse beschrieben berechnet werden
Beispielrechnung
Zur Berechnung des Volumens des Rotationskörpers der Funktion 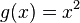 im Intervall von 0 bis 5.
im Intervall von 0 bis 5.
Hierbei wird die gegebene Funktion um die y-Achse rotiert.
Bildung der Umkehrfunktion
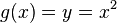
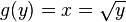
Berechnung des Volumens
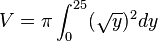
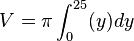
![V=\pi \Bigg[\frac{1}{2}y^2\Bigg]_{0}^{25}](/images/math/6/b/c/6bcb7cfe0545ef6351376bd2cf79b39c.png)
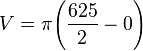
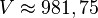
Interaktive Volumensberechnung mit Rotationskörpern
In folgender Anwendung kann nach der Eingabe einer Funktion sowie der oberen und unteren Grenze, das Volumen
sowohl bei der Rotation um die X- als auch um die Y- Achse bestimmt werden.
[ www.geogebra.org is not an authorized iframe site ]
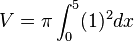
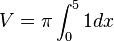
![V = \pi \big[x\big]_{0}^{5}](/images/math/3/f/a/3fa21bacf6598c2c57d01fa60aae3046.png)