Punkte, Vektoren und Geraden: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
| Zeile 1: | Zeile 1: | ||
| − | Ein Koordinatensystem eines dreidimensionalen Vektorraumes zeichnen wir, indem wir die x<sub>1</sub>-Achse 45° geneigt und um <math> {1 \over 2} \sqrt{2} </math> verkürzt zeichnen. Das heißt, dass (üblicherweise) auf den x<sub>2</sub>- und x<sub>3</sub>-Achsen 2 Kästchen eine Längeneinheit darstellen, während auf der x<sub>1</sub>-Achse eine Längeneinheit ein Kästchen diagonal repräsentiert. | + | Ein Koordinatensystem eines dreidimensionalen Vektorraumes zeichnen wir, indem wir die x<sub>1</sub>-Achse 45° geneigt und um <math> {1 \over 2} \sqrt{2} </math> verkürzt zeichnen. Das heißt, dass (üblicherweise) auf den x<sub>2</sub>- und x<sub>3</sub>-Achsen 2 Kästchen eine Längeneinheit darstellen, während auf der x<sub>1</sub>-Achse eine Längeneinheit ein Kästchen diagonal repräsentiert. [[Datei:Koordinatensystem3D.jpg]] |
Version vom 9. Februar 2012, 14:34 Uhr
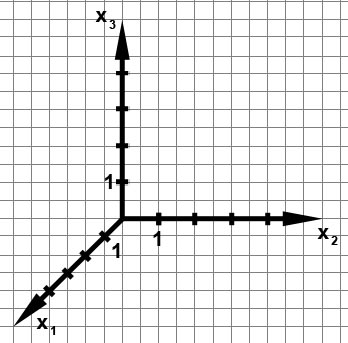
Ein Koordinatensystem eines dreidimensionalen Vektorraumes zeichnen wir, indem wir die x1-Achse 45° geneigt und um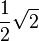 
verkürzt zeichnen. Das heißt, dass (üblicherweise) auf den x2- und x3-Achsen 2 Kästchen eine Längeneinheit darstellen, während auf der x1-Achse eine Längeneinheit ein Kästchen diagonal repräsentiert. 
