Punkte, Vektoren und Geraden: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
| Zeile 6: | Zeile 6: | ||
Im Arbeitsblatt kann dies nachvollzogen werden. Durch Veränderung der Koordinaten des Punktes P (mithilfe der Schieberegler) ändert sich auch der Ortsvektor <math> \vec{p}</math> des Punktes. | Im Arbeitsblatt kann dies nachvollzogen werden. Durch Veränderung der Koordinaten des Punktes P (mithilfe der Schieberegler) ändert sich auch der Ortsvektor <math> \vec{p}</math> des Punktes. | ||
| − | <ggb_applet width=" | + | <ggb_applet width="1200" height="661" version="4.0" ggbBase64="UEsDBBQACAAIANRgS0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADUYEtAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c627bRhb+nT7FgFsEydaXufKS2CmaFsUG69YCki26GwcBRY5l1hTJkNTNaR6qfZA+056ZISlKVGxJsZWkLRCL5NzP+c755sxwmKOvp8MYjWVeRGlybJEDbCGZBGkYJYNja1Se77vW10++OBrIdCD7uY/O03zol8cWVyWj8NgKA0favnD2scfFPudhsN8nPt+X2HGpTVnA+r6F0LSIHiXpj/5QFpkfyOfBhRz6J2ngl7rji7LMHh0eTiaTg7qrgzQfHA4G/YNpEVoIhpkUx1Z18wiaW6g0Ybo4xZgc/vzDiWl+P0qK0k8CaSElwih68sW9o0mUhOkETaKwvACBKbEtdCGjwQUI5XiuhQ5VqQw0ksmgjMaygLqtRy10OcwsXcxPVP49c4fiRh4LhdE4CmV+bOEDxpkjLJTmkUzKqgCpOjqsmzgaR3Ji2lJ3uhtuoTJN476vmkG//ooophjtqQsxFwoX2zZZ2KRhZi7UXLi5CFOGm+rcFOWmDDdlOLPQOCqifiyPrXM/LkBvUXKeA2bNc1HOYqnHUyXMRSZ7IFMRXUFh6M9CRtEw8D28x7H+MzK3BCStHst8tGGHdXeO46zXHf2Q7ljdHSfuYnf0fdLZ1yjU9L+OeES0tCnwnv6n/zo9MrpBj+b5wzq0+U5EPDqsveOocghUXKiyFYqlHBbKRZiHhKcsnSAB7mA7YNgCEQ8uDkXgAIgIxAU8EhfZ6uog5kAGRwy5SJUjDGl/EC78cEc3ZiMBjalUB9wQEeiII8EQ0W7EETgP0q4IbkkZlBACCaikuidUNcFsxG14Yi7iMEblhQ6BggwqwjN0TxEjiKnKxEHURrZqj3Dl3barhg5NUmRjZBPVIDgyOLFxYCjvIqaksSt1RUk2KhdUFAzD+rZMswYLKA0UNGc3Q0kL5HfvKPb7MoYJ4blCEqGxHytv0B2dp0mJahCpSRvkfnYRBcVzWZZQq0C/+GP/xC/l9HsoXdR967JBmhS9PC2/TePRMCkQCtIYN2NOY9K6p82o4YG1Mng7Q7Qy7Na9s7LfFHLQqJDQf5oXdXE/DJ+pEnNaAE2eJvHsaS79yyyNFsU4OtRzy5EcBXEURn7yExir6kXpBdVTjWapeqaxOasHkubh81kBFoym/5N5CnkEHxDbFa7wsMeIA2wzMznMYweCCgYzLRC7oIqSAl+5HsPeAeUOIQ4W2HYhY/aeHGabjuW4wcefyrmog1z5devhWfE0jedJWvpv/awc5TpGAB/OlUzfJINYagvRPAsTcHDZT6fPjWkw09aLWQZP2IygP9BaR8AMVMD8OKiufXPVZdTQmlKKbAbm0teXytyisClCPKrL6GvfXHUpsF8zukpaUktKcN1TVGhKw1blODVdKetXM/ooicqT+qGMgstK2qrCj6NhXzY2tNgmub021aghuCjKn1VoQYWlH/7bfnhxIUtfJYCFCM91HAG/1HNdY6xLZnp0KfNExpVXgEWM0lFhnHzeayiDaAhjN+mVTn0F+X9AApMaykEua8ljHcMZjetc3Lb3TrJu6vs8HT5Lxi/Ankxmy8PqQR4VQR5lym5RHyaSSzm3TBDdh3kobNdTXgxSBGq+Af2WSrfg36PyIgVrue8Ps8dBms0eo+8P0NOoLCVEt0kCbQFdQUnl1LEcQtiGSm26epwNfn/8pqNAGOuoEkccYGoL7lIuHM5s2zPiFbGKBdEwSjS0Q38K9ntAXUZcwbBDHE+4wN1+vwAeLCE6BkUm8+jYsFIdsmKsYm9ogbrqZgYRCdNJ59G0pQ6QMLoCQBeBVFaF0v4vQO9NBGCEmZeB7MahsHYnrJ0Jfv04u9CmRSq38mcgVxtJ3doPaVgphCy7XwlTwyWEvIWmibIiBH3zrygMZdLU8fNAsUc13zSGAnao0QTKzNRIMHG4YNSjgngehxvwApi+pHG7poMMhqoJqzUL+KNpFEd+Pls0d3ARA/pN8P++DD/E+oQT4YENMOF6jsfuFH+vxl/Yf+N/N/gH6RAYIUSJjmifJcAQBejOmkdZPsQr02+A6UE7EK7M9K3R46isC5yadqvWOnalJ9UGiVNrG6Q6s+McLLwmWPhatVTkXSjTw5Xl7eubK7NzYFbOSpQWbu3UJdpf8LNploNRKGArKceAHqQeW0WUPPjjt4cmWF3UWzIayjwKrFadJY+EAXqCYGELYoNpEFHHPxsY+To00Rn+pB7+fpAWavzon0hL8vtakkxWSYI9wT1YK1GXUEFtSncjyrQW5cGY7KEJeWgtmm1XmkV7npKtDJrgKpbDtAkK79KmV5lKbeMdxd+GzS9yy0+glzRfIpZTQypT0mEUSa6nlLFprlax3A6D95nT9do/PT8vZKl1SrnRId81OPMxbjH1tKLUwgTkgZ+XsoCguZpGS3juKYCNZ5yuwWe08qKKD9biM7oiwsAeJraa6hzucYeyHfEZXaTjDemsIwgARz3mQqhEbcJtymzh7IjOaENnFOiMbkxn9LOgs1WWUnlMV/E7pjPapTO6GZ1th8F2dLYT7X9svrqeh1iXh/CKBcXi9kYr0r6DJUV3JUBudeHXZUDWJvA1eW+F4pbmMbEj1mMN6zFgPbYx67HPhPXMwmSFmnfMcazLcWwzjttO4x8asrlGf3eLwyfNdr3XncUXPhAfZ/+kZtnWBtI+rXaQ6PY7hoKtu2G01c5Nd5Nm3U2ZTVBaERz/uVBy197W/YRRWjED/rlQItj9HGDqLkh7VUQAfAeruTFBXyFwKnVL9S1Tt2ytdWpvxfKOUYKJ59jYszHBbNPNqhuCscXBT+aDn8wHP1lr8JPO4CFGd7HLbOIx23aJJxi/1cH3mlCsB6FYb9NQrLdVXEAxv53Vz8KmTAdkM+l39Xc3m8S912+ne7N3tT5XWPIeWmEhG2u86uaGBc9db8zfrHlIJx63PYptzh1YaJI70/x0WelzTW+s3uknpVnuCEFdKkB5jnBst9lo5I7DhSMIx7B6Z4TclWpnc9XOjXhLy519OqoF2xRcYJd7DnEd7gBBNEYLNstBpQw7oFeXunewWnsuByp9abnWMIhatIG2lhdt/de961dtRdVsrU9V4Xp+3nBf5ENMeYXJan7umrhZlDkOFZxyV3gM4HHFOmELWR23yDfJwhotGmZxFERlo+FYRSvNG1Ww/2Lp1Me9o0spM3Vm6DR5kftJoQ4fd06GfAjcHbSDTdEOPiW0l1B1KrDNG1rlZUIdTPBsB2YNhj3WORv1WcH7ZiTV2e5FfCvUX+oGY7+UL0/3kNmneSkJOkQCaPTy1as9NC8xpSuLvDJGcgkXqiNtn8HIYlD4g+8ic7D85RRmvdNXUOdEJoPyAuq/gsriYcewTqIkkgkYH9jetQYWQ9ON7bRrbWVlRDBtZ4J8qKFts3RZj7b3OxHz3SHNdoj01VZIX22JNF7YZv3LAE3fAzRZWWQtoOkS0PQGoGfTbYBWtf526VtAmu0Q6a1ceratS9/qu5PPC2x2s1uzDcFmS2CzG8C+2sqtr7Z1678of78PaLpDoLcKya62Dsn+LF69cnk1rVZW1TJrWef+pusr/5NZX63cpJi9Z1fj81pN33zwvZ+msfSTOSzLW+atbnb9wlp4Bgj7Whz9TL9D0WmneVmM5SWwC/KTKxkNZHLzrtwLOS15tTF3/80oLR//W9lGlABfJYX5givM5YVMHplsq7s3V0Ib1mKDH9O4V7/xQkqpxByvZJ5YTzN0QTMtBX95NpbB2+zdl+hqNES9UXJZot6j+/8g+LHJQxk6PovlefngrC8HUfLWz3N/9u5t8M60hb5CD078F/Lnl73X5NVDeDTpZ2fdfHpDPmvlozOZhFVnZ/oTtodVzqpd1Q5yNx1AW/zYMIzMGzz1HWFV2r8zWKNCy7t8OEN/q1nIPDqff9eov87DVs0qa9hF9c6TeddPD9cdjeluu2XXTwpLB2Oytd9/ra35+gPE7VmoOufsrb1Zt9Gbs499Xmalz5MFn69dG/UeNI6nXgjV/vZrK5WuTGVN6sMNHPGmg+0fjUI9jSjtvJU4bH+UqJ7r//Hiyf8BUEsHCOe8GlrbCwAAjkMAAFBLAQIUABQACAAIANRgS0BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA1GBLQOe8GlrbCwAAjkMAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABzDAAAAAA=" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> |
== Vektoren im Raum == | == Vektoren im Raum == | ||
| Zeile 14: | Zeile 14: | ||
Mit den Schiebereglern können wieder die Koordinaten der Punkte P und Q verändert werden. | Mit den Schiebereglern können wieder die Koordinaten der Punkte P und Q verändert werden. | ||
| − | <ggb_applet width=" | + | <ggb_applet width="1200" height="663" version="4.0" ggbBase64="UEsDBBQACAAIAPlgS0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAD5YEtAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c63LbNhb+nT4FhtvpOFtfCIDgJbHb6WU6m1m3libZTneTTIaiYJk1RaokdU3zUO2D9Jn2ACApUqRlSrEUO+lMYt5A4JzznfPh4EKdfj0bBmjC48SPwjMNH+sa4qEX9f1wcKaN08sjW/v6q89OBzwa8F7sossoHrrpmWaIkn7/TOt7FjddZh3pjsGODKPvHfWwaxxx3bKJSahHe66G0Czxn4TRT+6QJyPX48+9Kz50zyPPTWXDV2k6enJyMp1Oj/OmjqN4cDIY9I5nSV9DIGaYnGnZyROorvLSlMriRNfxyS8/nqvqj/wwSd3Q4xoSKoz9rz57dDr1w340RVO/n16BwgSbGrri/uAKlLJ1UOpElBqBRUbcS/0JT+Dd0qVUOh2ONFnMDcXzR+oMBYU+Gur7E7/P4zNNP6YMY4YpZpbtGBa1NBTFPg/TrCzO2jzJazud+HyqqhVnskVDQ2kUBT1X1Ih+/x0RnejoUBywOhA4mKZ6pKt7OlUHog6GOjBVxlCvG6qoocoYqoxBNTTxE78X8DPt0g0SMKEfXsYAX3GdpPOAS3myG0vt8SHolPgLKEyESZXNQfBD/dDQ5X+lc0lBXGoxjccbNpg3Z5l2u+bI+zRH8+YMYlWbIzdpZ64xqGq/jXqYlazJ9EP5T/6vtUjJBi2q6/dr0DT2ouLpSR4dp1lAoORKlM1QTPkwESFCHcQc4ekYMQgH0wLHZgg7cLAIggBAmCGDwSW2kSmOFqIWPDAQRTYS5TBFMh6YDX8MS1ZmIgaVibsWhCHC0JCBGEVYhpGBIHiQDEUIS0KhBGOIwUuieUxEFdREhglX1EYGyCii0MJQkMKLcA3NE0QxouJlbCFiIlPUhw0R3aYtRIcqCTJ1ZGJRIQQyBLEKYChvIyq0MTNz+eFonFZM5A37+WkajQosoDRQ0JLoFCVVePDRaeD2eAB9w3OBJEITNxDRIBu6jMIU5SASdW8Qu6Mr30ue8zSFtxL0qztxz92Uz36A0knetizrRWHSiaP0uygYD8MEIS8K9ELmKMClc1JIDRe09MAoP2ClB2bp3GpsN4InaJxwaD+Kk7y42+8/EyWWtACWvAiD+bcxd69HkV9V4/REdjOnfOwFft93w5/BWUUrwi4o73UkS+WdjmmwXJAo7j+fJ+DBaPY/HkfwDOvH2LSZzRzdodhiGpqrJ9Shx4wwCp0uEDsjFPBOPFfEHtWdY2JYGFs6002bOPBS8yNKDNU0nxQIuTO+VHYQi8guXTxLvo2C5S2p/3fuKB3HMmGAKI6FVt+Eg4BLH5FMC72xd92LZs+Vc1BV14v5CK50JUFvIO2OgBsIAzUH2bGnjrKMEK0oJehmoA49ecgczu8XRbBDZBl57KmjLAUerKTLtMW5pljPW/ITSWq6loVOTljC/0X3Pg799Dy/SH3vOtM2e+Gn8bDHCy+q1onvrk4hNWQaSfqLyDMI0+TFf8sXL6546oob4CPMsS2LwV/i2LZy1xVHPb3mcciDLC7AI8bROFFhvmy1zz1/CLKr+5lNXQH5f0ADdbfPBzHPNQ9kQqcsLp/qZY+v3ZZV/RBHw2fh5AX4k3pYirFcyNPEi/2R8FvUg67kmi89E1R3oSfql98TcQxaeKLHAfumwrYQ4eP0KgJv+cIdjp560Wj+FP1wjL7105RDqhuGUBcQFpQUYR3wISRuKJWuK+Us8PvrD5kSgqzjTB12rBOTGTYxmGVQ03SUekkgEkM09EMJ7dCdgf8eE5tim1HdwpbDbIhmt5cAE6aQKoMhw2WqrHgpz191XSTiUAOxxckcchIqb136s5I5QEN/AYBWgRRehaLer0DwRQ6glFmWgcdFQOkynHQZTPDXDUZX0rVwFlbuHPQqIylr+zHqZwbBq+GXQudwDUlvImkizQhBnvzL7/d5WLzjxp5gj6zHKRwF/FCiCaQ5EpLo2DIYJQ5h2HEMOIEogA6Mq7ArGhiBqJKwSv2AO575ge/G86q7Q4go0G+D/89V+CHxxwZmDvgAZbZjOXSn+Ds5/sz8G//d4O9FQ2CEPgplTvssBIZIwHbaMs9yIWOZfQNMD9aBhGUuT5Udx2le4ELVm9VW8yvZqRZIXGjbIFXrHZdg6S3B0teaJSPvRLiennnekTxZqGkENYwWqpRwK99dof1KnM1GMTiFADbTcgLowd0zLfHDg7/+eKzS1ardwvGQx76nld5ZiUgQ0GFYZybDJrgGZpA1berkbWiiJv40F//IixIhP/onkpr82UqTaZMmusMMB0ZLxMaEEZOQ/agyy1U5mOBDNMWPtarb1rWp+vMMb+XQWM9yOZ0USeEufbrJVXIfrxn+Lny+yi0/g12ieIVYLhSpzHCNUTheTykTVV1uYr4dBje503rrX1xeJjyVNoXhhrShsW9wljJu0fWUstREJeSeG6c8gaQ560ZTuO4IgFVkXLTgM5JFUcYHrfiMNGQYuqNjU3R1luEYFqF74jNSpeMN6aymCABHHGpDqkRMbJgwmmXWnuiMFHRGgM7IxnRGHgSdNXlKFjF1w++ZzkidzshmdLYdBtvR2V6s/6H5aj0P0ToP6Q0Diur0RinT3sGQoj4SwHc68KszIC0TeEveazDcSj/G9sR6tGA9CqxHN2Y9+kBYTw1MGsy8Z46jdY6jm3HcdhZ/35TNVvbbLQ73mu06b2qDr2a628P8Sd5saQLpiGQzSGT7GUNG204YbTVzU5+kaTspswlKDcnxx4WS3Xpa9x6j1DJ1eLgoYd1+CDDVB6SdLCMAvoPR3ASjLxEElTgl8pSKU9pqnNq5EeTWAN6SfFWFnS6FnS6FnbYSdrpzYTtFqtWBVKuzaarV2arfJ7pxN6Obpk58V5O8nTdvZ4fzd7m9GjzxEDUgvrFFs2ZuGbDsemJ9r/PnndmqVZem3Nh+s/tjuqN92G6+tN3SDbf0vfn9sd2dm646HnrOB+L+yoCoiHExLAJrrA6Lem8668dFSVZtbi/xwnqG3HDm4c4IsuWwBjf39Py3sDKq8YejwPf8tLBYIPr3Yg0S/DVZ2Sfx6PSa85HYZXMRvojdMBF7d2t7Kd4Hvhp63qboefcGvaOPDb7fxlxsfa7il6H6UlYYuCl/eXGI1MzFS47RCWJAa9evXx+iZYkZaSzyWjnBNRyIzD1dCpIFYNCD73217/rlDLqZi9fwzjkPB+kVvP8aXmaPa45z7oc+D8G5wLfWOlAAVRe+UX5rKy/CjEo/Yvh9HWmbZL4dzR7VcszdIU33iPRiK6QXWyKtVyYePxmgyQ1A48YirYAmK0CTW4Cez7YBWrz1d0jfAdJ0j0hvFdLzbUP6TlcTHhbY9PawphuCTVfApreAvdgqrBfbhvUnyt83AU32CPRWKdli65TsY4nqxuHTLBs5ZcOoVZu7m46f3HszfnpAw6fbt3b3oijgbrg08+okcamZfS/JMkctypprcXFHcpVA3vuZxz0/7I/DQTLh10AayA0X3B/w8PbJrxd8lhrZ/NcXv42j9Om/BeR+CDQUJupjpX7Mr3j4RD3W6lNgKdShVSv8kD7bvLSDhG2x2kdIHbbeP1ZXEbr1ReJiMu2BL2yxfGHLJg9hYesWmGqrxB8LTGYGE8H4I4Cptkz80cFkPAiYGruDSm/QGYfXKeoeIHWJvkTAhfBXXf5euksa7h505VKtun6cHZpWUWpdyH3tQRxFlqzFwrBQAzcYs3NQ2KfTaMtOoy3FqveXVVO2suRt3wJ8YFOSFit0szejzI7C+Y6E2dqs/YvXbuKZO1r8n5ckI1Iy0kay+e4lW5Qko1KyVvslFruXTDglqcRFPYH9/FU04bH81tyN42j6ttN99zmaQCUdtBij7pMv/oH1p43F0NmrgF+mB696fOCHb+G+O3/31nu3JKVz9wX/5SV4x+vHRUS9erX6fH7L80XlOXrFw37W2Csp0GO0QZDetsO9+nsGfV9xv/ipgqy0u7MI9hOp7+ruT/lzEAn4zuXypxPk5/+6lg/qWuTjWW9p1UlgfQbRcs/mh9yifrcb1Nebo+XmyE/FHA/gA4Ydf74w6ZY6zGyTVXe53a+7yXa/bsPXXKZBdBhFE+yI36nKf53jrrb/VYWfLoWfLoVvuf2vJrx+zExsWoTaFqUmdfRNP0RbL3u32A3YPUTT7qb7h7of+Gvwyn6JGshq/q9mv91sy+oWW9q6xZa27pZb2rr3a0vbfr88bjDtfGnafMdbd8sdb917teNtz19BNpi2use1gX6XXlyitY2tft/2uN5EF3AfDE9tAxPbYbZlEntvexG72WpM98bVmO6mqzG38fP+VmMaHHp+QwQsGu7nn+g/iMWbVmCXdy52mzaebgh2796A3dwzNH1vZ36SYNew9jbF2rtPWK9galSWXQXPYt3EQKVYB1KlFn244DZ+Utu5CdXRekxXPqgd7WBGJf/lwu0Xd7NO0dlJDr7f72w7q9ielH9/T1znv/T81f8BUEsHCN3S/6wQDQAAhloAAFBLAQIUABQACAAIAPlgS0BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA+WBLQN3S/6wQDQAAhloAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACoDQAAAAA=" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> |
== Geraden im Raum == | == Geraden im Raum == | ||
| Zeile 25: | Zeile 25: | ||
Im Arbeitsblatt können die Koordinaten von P und <math>\vec u</math> mit den Schiebereglern verändert werden. | Im Arbeitsblatt können die Koordinaten von P und <math>\vec u</math> mit den Schiebereglern verändert werden. | ||
| − | <ggb_applet width=" | + | <ggb_applet width="1200" height="661" version="4.0" ggbBase64="UEsDBBQACAAIABxhS0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAcYUtAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dW3PbyJV+nvyKLsY1ZW106SsuHmlSmaRmd2qdiFo5Ke3arikQbFGISIADgDd5/KOS57zlPb9pT3cDIEhAIkBLNOVJlW3cGuhzznfOd043mvDpb+ejIZrKOAmi8KxDjnEHydCP+kE4OOtM0usjp/Pbb391OpDRQPZiD11H8chLzzpctQz6Z52+b0vLE/YRdrk44rzvH/WIx48kth1qUeazntdBaJ4Er8LoT95IJmPPl5f+jRx5ryPfS3XHN2k6fnVyMpvNjvOujqN4cDIY9I7nSb+DQMwwOetkO6/gcSs3zZhuTjEmJ1d/fG0efxSESeqFvuwgpcIk+PZXX53OgrAfzdAs6Kc3oDAlVgfdyGBwA0rZrtNBJ6rVGCwyln4aTGUC95YOtdLpaNzRzbxQXf/K7KFhoU8H9YNp0JfxWQcfM85s0UFRHMgwzRqQrKOT/BGn00DOzLPUnu6Gd1AaRcOepx6Dfv4ZUUwxOlQbYjYUNpZlLmFzDjOzoWbDzUaYNtzczk1Tbtpw04azDpoGSdAbyrPOtTdMwG5BeB0DZsVxki6GUsuTnViqTA5BpyS4g8bQXwcZQ4Pgh/iQY/3X6FxSkJR6TONJyw7z7mzbbtYd/ZTuWN4dJ85qd/Q+7awHDGr6b6IeESVrCnyo/+i/lR4ZbdGjOf60Di2+ExVPT/LoOM0CAiU3qm2GYipHiQoR5iLhKk8nSEA4WDY4tkDEhY1NEQQAIgJxAYfEQZba2ojZcIEjhhyk2hGGdDwIB/7htn6YhQQ8TJ21IQwRgY44EgwRHUYcQfAgHYoQlpRBCyGQgJtU94SqRzALcQuOmIM4yKii0CbQkMGNcAzdU8QIYupmYiNqIUs9j3AV3ZajRIdHUmRhZBH1QAhkCGITwNDeQUxpY2XmCsLxJF0xkT/q57tpNC6wgNZAQUt2M5S0Qn5fnQ69nhxCQrhUSCI09YYqGnRH11GYohxEas4NYm98E/jJpUxTuCtBf/Wm3msvlfPvoXWS963b+lGYdOMo/X00nIzCBCE/GuJC5mhISvu0kBoOWOkCL18QpQtWad+u7TeCK2iSSOg/ipO8udfv/6BaLGkBLHkeDhffxdK7HUfBqhqnJzq3nMqJPwz6gRf+BZxV9aLsgvJUo1kqzzQWZ7kgUdy/XCTgwWj+fzKO4BrBx8RyhCNc7DJiA9sszBXmsmNBBYNMC8QuqKIk31Ohx7B7TLlNiI0Fthy4sLjnCrNMx3Ja4OPN5VLVQaziunTwQ/JdNFye0tr/3hunk1jXCBDDsdLpd+FgKLWHaJ6FBOzf9qL5pXENZp71ZjGGI2wk6A201REwAxWQHwfZtme2uo0SrWilyGZgNj29ydwt6BdNiEt1G73tma1uBf5rpMu0JbmmBOc9BYmmNNzJAienK+X9KqNPwiB9nR+kgX+baZvd8KfJqCcLH1p9Jnm8ZyqpobhI0itVWlDR0Qf/Wz54cyNTT50ADxGuY9sC/qWu4xhnXXPT01sZh3KYRQV4xCSaJCbIl732pR+MQHZzPrOppyD/M2hgzvblIJa55kNdwxmL66u47O+V0/pR38fR6Idw+gb8yVwsRVgu5Gnix8FY+S3qQSK5lUvPBNU9yEP98n0qikELX+UbsG+qbAvxPUlvIvCWr73R+Bs/Gi++Qd8fo++CNJVQ3YYhPAvoClqqoB7KEZRtKNWuq+Us8PvX33QVCLJOMnXEMaaW4A7lwubMslyjXjJUtSAaBaGGduTNwX+PqcOIIxi2ie0KB7jb6yXAgylUx2DIcFkdG1bKS1aMVe0NT6C22llAr9RSe9fBvGQO0DC4A0BXgVRehaLeX4HeiwrAKLNsA5eLgMI6nLAOJvjXG45vtGuRLKy8BehVRlI/7Y9RPzMIWQ+/FFLDLZS8iaaJNCMEvfNfQb8vw+IeL/YVe2T5pnAU8EONJlDmWEmCic0Foy4VxHU57EAUQPqSJuyKDsYgqiasUhbwJvNgGHjxYtXdIUQM6Jvg//s6/FDrE06ECz7AhOPaLntS/K0cf2H/G/+nwd+PRsAIfRTqivaHEBgiAdt1llWWB/XK/HfA9GAdKFcWetfYcZLmDc7Nc7OnVfxKJ9UCifPONkhVsuMSLNwQLPygWTLyTpTr4czzjvTOnZk5MCNnpUoJt/LZNdpfibP5OAanUMBmWk4BPTh71kmC8OW//nZgitVVu4WTkYwDv1O6Zy0iQUBXECwsQSxwDSLy+qeFkzehiYr4s1z8Iz9KlPzoP5DW5O+NNJnVaYJdwV0YK1GHUOB8SnejyjxX5eWUHKIZOeisum1Vm1V/npOtHJrgrJbDtCgKn9Kn61wl9/GK4R/D51e55S9glyheI5ZzQypzUmEUSR6mlKl5XG5iuR0G97nTw9Y/v75OZKptSrmxId81OEsZt0g9pSo1MQW578WpTKBoztJoCsddBbCJjPMGfEazKMr4oBGf0ZoKA7uYWCrV2dzlNmU74jO6Ssct6ayiCABHXeZAqUQtwi3KLGHviM5oQWcU6Iy2pjP6LOiszlOyiKkafsd0Rqt0RtvR2XYYbEdnO7H+5+arh3mIVXkI1wwoVqc3SpX2EwwpqiMB8qgDvyoDsjKBN+S9GsOt5TGxI9ZjBesxYD3WmvXYM2E9MzCpMfOOOY5VOY6147jtLP6pJZtj7Pe0OOw123V/rAy+6uluB/MnebelCaQjms0g0fYzRk4+Y8SaThhtNXNTnaRpOinTBqWa4vjLQsnBXwBKDUuH54sSwc5zgKk6IO1mFQHwHYzmpgT9BkFQqV2qd5naZY3Gqd17QW4M4Ibia1XY2VLY2VLYWSNhZ08ubLcotbpQanXbllrdrfI+xfxxRjd1SfypJnm7P36YHy4+5vaq8cRDVIN4a4tm3WwYsDz1xPpO58+783WrLk3Z2n7z/THd0S5st1jabumGW/reYn9s9+imWx0PXcqBOr82ICpiXA2LwBrrw6Lej92Hx0VJ9tjcXuqGhxmy5czDoxFkw2ENqc/08qdwZVQTjMbDwA/SwmJDld+Ld5Dgr8naOomvTm+lHKtVNufhm9gLE7Vct7KW4lPgq6Dnt0XP3xv0jp47fA/XOZO6Yaz4IkrvfOED5c9/hDSpG8d+YTBZjden7DFMNQPZLwwmlz97mNK9AYnUgCQykMT2IDGxY5CavlXZMNlwUR6N/AZBcjrIh3q6yFan6EE++fBSDejVKXbQfBLiouYdM6MEE9e2sGthglnbFTMbJiXqlZpVlZpVlWo4WVFRCh9TBzvMIi6zLIe4gvFHVarQaXpxiGYXbYc7F5958dpKeVdB31R7VQPu6N1Q11TRF5UqevJwDb32ZmjymdbyZINHKp4GgN2+FOo2IK2r1fhOIWxriMucrpCXOd2GwK5qCIxYWGDXcTB3MBak7erFDQR2v4KzegVn9Qo2JLOKgiAlx5w44B8O4xg8pe0ioIcVLPSbXgGZXbUls6vtZmKzX7M87lC14ggmlKr229W8ztV9UwL9dhMC/T2ZDqi1pbFxxfR32ezB1nT1pJMFmxeyX8qfJlL9MnoV0gzot/p5Qy+Vb88PkclkbyVBJ0hArN++f3+Ili3mtLbJe+Mdt7ChunT0GAg/BGu//ENgfpb9dk4O0fl7uOe1DAfpDdz/Hm4WBxWPeh2EgQx//DBffHzYt4bw6MJxyndt5WJEMO1kgnyql23jIs1C96jCgk+HNNsh0ndbIX23JdJ4ZZHSLwZoeg/QpLZJI6DpGtB0A9CL+TZAq7v+HdKPgDTbIdJbhfRi25B+1JWHzwtstjmsWUuw2RrYbAPYd1uF9d22Yf0L5e/7gKY7BHqrkuxu65LsuUZ1zURbsUBjfU70EK1PKLaehduvBRvcFoI6VDgE9mzLKRYhcNvmwhYw8LKoxQh5ovUcF4uSqVfmmg8rE7WtTb1X6zuI4AI73LWJY3ObWSQ3NeGWy8HEDNtgZ4c6T2Xq1RVdDab7q95eM33eGpV9W/F132SoggaAcSm2OLddBiGyu5U582wKJzPWOsd7bdd2eHuztuMZLe1oMltTh95Fht7FvehdtEVv08ubXU7FVehqcQ+/GXRtmwpOuSNcBqcd8cWhXV6GdVG3iq4l2r29Qbu+ENBwVwuHXyLaFbD9tmD7+wT2Gqj2ClGrfCjU93Ncy4ZUybDLKp/w2md0a95Brdf5K68Ri+pn5d1b6xdV+1XvUwbYcUJdYG/bcXhR71Pm2NQB1DFQOxHicX6VWWPz9YJ/5R3tYe2LzdY236vCf50Si8IfIIBESQSElCWE+0jlZY3Jawv/Jq/M60PgntfPrVHaw4FA7atc/SUTwAo4j1JgP4id3b3KzUrJq3tLyXnbUrKGkJrkmyd4d14bAot7YsaUF8QFehIWJdzhjFPSKAOxPclAjQAv1xdXddVkS8B7ewT4PYnGrDyqZKZfJOI1FWVLwP39AnwNV2atF5WYOcRi3CUuxxD3jD1fgF+DzPULC6u4DjZNzodLwAaNVzv5UdgPzCph9WXkrLF3P9j5h33Va9fHSaG1S3Vqc+unrix8GG3fG2tDaEn/U8YeSC2D8E4G/k0ow0rdtGL+XhQNpRcu0+b6+riSw+x6uadwzZyL9SAmNdp7SvlBjeqVkvGNnKf5twW//mkSpd+8vEz/+Y/07uigOwlvU9RFau28ee4r1H1pGukfAqv60Bz+XDpLa86+ND8ON8cH2aaucExBnM6qbJ9zzFz/CwGksHHN7zUaVOVKDbpi4v8Bx0wn4SCZytsUBH7xbir9D5OPL8q2/vrXBH9jLqEJOns3lNfpy3c9OQjCD14ce4uPH/yPSwu/9t7Iq7dQur8/KAB49656nW64zkrX0TsZ9rPO3ulPjB9kVxpht+kDYU+LXZBolVYZPftcfiLj4Hr5aXn9gXTcydllM/jEzGwT5jaDn63Af5nG0r9V+F97Gv/0VWbVBkbd9EWizxYQWUnPKG1mE75ik/9WmSUIvVSGifkUfz+WNzJsYRm+t5Yx3sJd0WQIT0pf2SjG402Wdl/V/diUtv222SbxaCFeaV6gmXg1P7J8dPFYIV5peXwz8Wp+XPjI4ikvFStufx6neRK4m4yQSblXr5Am/xdIk/+H+Ud0hpBJAGhTBrjakAGuNmSAq00Z4AUI86KhMN0NwnQ3CNPdmI6Ka8U9afmJzcR88qzZImmKzzyk++S0WfqRjx4okGOX2QLbnFrcdS2XFC8bhP5fubDgnHJGMbfKk23lSDop/x8S6jj/D8q+/X9QSwcIjrzX3VgPAAA9bQAAUEsBAhQAFAAIAAgAHGFLQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAcYUtAjrzX3VgPAAA9bQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPAPAAAAAA==" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "false" allowRescaling = "true" /> |
| + | <br /> | ||
Alle Punkte X zusammen bilden die Gerade. Der Vektor <math>\vec x</math> ist der Ortsvektor zu jedem Punkt X der Gerade. Der Parameter t ist nötig, um jeden Punkt der Gerade beschreiben zu können. | Alle Punkte X zusammen bilden die Gerade. Der Vektor <math>\vec x</math> ist der Ortsvektor zu jedem Punkt X der Gerade. Der Parameter t ist nötig, um jeden Punkt der Gerade beschreiben zu können. | ||
Version vom 11. Februar 2012, 12:09 Uhr
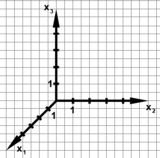
Ein Koordinatensystem eines dreidimensionalen Vektorraumes zeichnen wir, indem wir die x1-Achse 45° geneigt und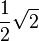 
verkürzt zeichnen. Das heißt, dass (üblicherweise) auf den x2- und x3-Achsen 2 Kästchen eine Längeneinheit darstellen, während auf der x1-Achse eine Längeneinheit ein Kästchen diagonal repräsentiert.
Punkte im Raum
Punkte im dreidimensionalen Vektorraum haben drei Koordinaten. Diese werden waagerecht geschrieben. Vektoren dagegen werden, mit = getrennt, senkrecht geschrieben. Ein Ortsvektor ist dabei ein Vektor, der die Verschiebung vom Ursprung zum entsprechenden Punkt beschreibt.
Im Arbeitsblatt kann dies nachvollzogen werden. Durch Veränderung der Koordinaten des Punktes P (mithilfe der Schieberegler) ändert sich auch der Ortsvektor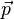 
des Punktes.
Vektoren im Raum
Ein Vektor stellt eine Verschiebung eines Punktes im Raum dar. Der Pfeil repräsentiert dabei den Vektor, wobei jeder Vektor durch unendlich viele Pfeile repräsentiert werden kann; abhängig davon, wo die Verschiebung beginnt.
Im Arbeitsblatt stellt der Vektor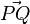 
eine Verschiebung vom Punkt P zum Punkt Q dar.
Mit den Schiebereglern können wieder die Koordinaten der Punkte P und Q verändert werden.
Geraden im Raum
Geraden werden mithilfe einer Parametergleichung beschrieben. Das Arbeitsblatt zeigt alle dazu nötigen Elemente:
- ein Punkt P der Gerade; der Ortsvektor zu diesem Punkt ist der Stützvektor
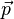der Gerade
- ein Vektor, der die Richtung der Gerade, von P ausgehend, beschreibt; dieser Vektor ist der Richtungsvektor
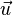der Gerade
Im Arbeitsblatt können die Koordinaten von P und 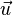mit den Schiebereglern verändert werden.
Alle Punkte X zusammen bilden die Gerade. Der Vektor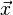 
ist der Ortsvektor zu jedem Punkt X der Gerade. Der Parameter t ist nötig, um jeden Punkt der Gerade beschreiben zu können.
