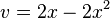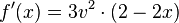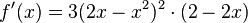Ableitungsregeln: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(→Quotientenregel) |
(→Kettenregel) |
||
| Zeile 26: | Zeile 26: | ||
<math>f'(x)=u(v(x))</math><br /> | <math>f'(x)=u(v(x))</math><br /> | ||
<br /> | <br /> | ||
| + | Beispiel:<br /> | ||
<math>f(x)=(2x-x^2)^3</math><br /> | <math>f(x)=(2x-x^2)^3</math><br /> | ||
<br /> | <br /> | ||
| Zeile 33: | Zeile 34: | ||
<br /> | <br /> | ||
<math>f'(x)=3v^2\cdot(2-2x)</math><br /> | <math>f'(x)=3v^2\cdot(2-2x)</math><br /> | ||
| − | <math>=3(2x-x^2)^2\cdot( | + | <br /> |
| + | <math>f'(x)=3(2x-x^2)^2\cdot(2-2x)</math><br /> | ||
Version vom 6. März 2012, 08:45 Uhr
Bekannte Ableitungsregeln aus Klasse 10
Potenzregel
Summenregel
Faktorregel
Neue Ableitungsregeln
Produktregel
Allgemeine Formel der Produktregel
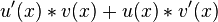
Quotientenregel
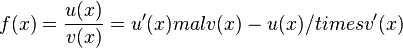
Kettenregel
Allgemeine Formel der Kettenregel:
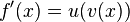
Beispiel:
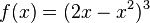
äußere Funktion: 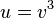
innere Funktion: