Tangentenprobleme: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(→Tangente - Definition und Tangentengleichung) |
(→Tangente an Schaubild anlegen, Berührpunkt ist bekannt) |
||
| Zeile 9: | Zeile 9: | ||
== Tangente an Schaubild anlegen, Berührpunkt ist bekannt == | == Tangente an Schaubild anlegen, Berührpunkt ist bekannt == | ||
| + | |||
| + | {{Aufgabe|1= | ||
| + | Bestimme die Gleichung der Tangente, die am Schaubild der Funktion <math>f(x)={1 \over 9} x^3 -x</math> an der Stelle <math>x_0=3</math> angelegt werden kann. | ||
| + | }} | ||
== Tangente an Schaubild anlegen, Steigung ist bekannt == | == Tangente an Schaubild anlegen, Steigung ist bekannt == | ||
== Tangente an Schaubild anlegen, Berührpunkt unbekannt == | == Tangente an Schaubild anlegen, Berührpunkt unbekannt == | ||
Version vom 24. Mai 2012, 21:38 Uhr
Tangente - Definition und Tangentengleichung
Eine Tangente berührt das Schaubild in nur einen Punkt. Leider ist diese Definition nicht vollständig. Besser ist:
Definition
Gegeben ist ein Punkt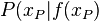 
auf dem Schaubild einer differenzierbaren Funktion f. Die Tangente des Schaubildes im Punkt P ist genau diejenige Gerade durch P mit 
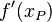als Steigung.
Tangente an Schaubild anlegen, Berührpunkt ist bekannt
30px Aufgabe
Bestimme die Gleichung der Tangente, die am Schaubild der Funktion |
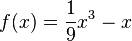an der Stelle 
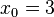angelegt werden kann.
