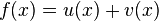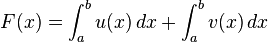Die Stammfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Definition der Stammfunktion === Die Funktion <math>F(x)</math> der Ausgangsfunktion <math>f(x)</math> heißt Stammfunktion. <math>F(x)</math> ist die differe…“) |
(→Integrationsregeln zum Berechnen der Stammfunktion) |
||
| Zeile 31: | Zeile 31: | ||
=== Integrationsregeln zum Berechnen der Stammfunktion === | === Integrationsregeln zum Berechnen der Stammfunktion === | ||
| − | Um an die Stammfunktion zu kommen muss man die Funktion <math>f(x)</math> integrieren. Dabei muss man bestimmte Regeln beachten von denen die meisten den bereits bekannten Ableitungsregeln sehr ähnlich sind. | + | Um an die Stammfunktion zu kommen muss man die Funktion <math>f(x)</math> integrieren. Dabei muss man bestimmte Regeln beachten von denen die meisten den bereits bekannten [[Ableitungsregeln]] sehr ähnlich sind. |
Version vom 4. November 2012, 20:01 Uhr
Inhaltsverzeichnis |
Definition der Stammfunktion
Die Funktion 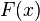 der Ausgangsfunktion
der Ausgangsfunktion  heißt Stammfunktion.
heißt Stammfunktion. 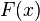 ist die differenzierbare Funktion der reellen Funktion
ist die differenzierbare Funktion der reellen Funktion  im Intervall
im Intervall ![\left[a;b\right]](/images/math/3/1/9/3195fbba6a681f201877c58390e7a641.png) , sodass gilt:
, sodass gilt:
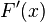


Jede Funktion  hat unendlich viele Stammfunktionen.
hat unendlich viele Stammfunktionen.
Auf die Stammfunktion kommt man, indem man die Ausgangsfunktion integriert, also:
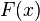

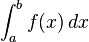
Stammfunktionen zu einfachen Funktionen
 |
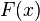
|
|---|---|
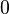 |

|
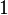 |
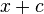
|
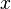 |
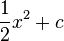
|
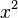 |
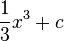
|
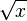  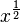 |
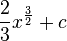
|
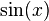 |
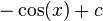
|
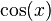 |
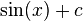
|
Integrationsregeln zum Berechnen der Stammfunktion
Um an die Stammfunktion zu kommen muss man die Funktion  integrieren. Dabei muss man bestimmte Regeln beachten von denen die meisten den bereits bekannten Ableitungsregeln sehr ähnlich sind.
integrieren. Dabei muss man bestimmte Regeln beachten von denen die meisten den bereits bekannten Ableitungsregeln sehr ähnlich sind.
Potenzregel
Möchte man eine Potenzfunktion wie zum Beispiel 

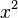 integrieren um an die Stammfunktion zu kommen, so gilt:
integrieren um an die Stammfunktion zu kommen, so gilt:
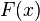

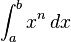

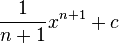
Beispiel: 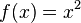
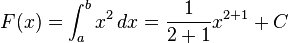

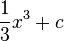
Summenregel
Möchte man eine Summe von zwei Funktionen integrieren so gilt die selbe Regel, wie beim Ableiten:
Summenregel beim Ableiten:
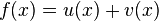
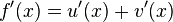
Genau wie beim Ableiten werden beim Integrieren die Summanden einzeln integriert und dann stehen gelassen oder vereinfacht.