Abstandsberechnungen Punkt-Gerade und Punkt-Ebene: Unterschied zwischen den Versionen
(→Abstand zwischen einem Punkt und einer Ebene) |
(→Abstand zwischen einem Punkt und einer Ebene) |
||
| Zeile 181: | Zeile 181: | ||
Basierend auf der Hesse’schen Normalenform HNF lässt sich der Abstand eines Punktes und einer Ebene berechnen mit:<br /> | Basierend auf der Hesse’schen Normalenform HNF lässt sich der Abstand eines Punktes und einer Ebene berechnen mit:<br /> | ||
<br /> | <br /> | ||
| − | <math>d= \left| \frac{\ a_1x_1+ | + | <math>d= \left| \frac{\ a_1x_1+a_2x_2+a_3x_3-b}{\left|\vec{n} \right|} \right| </math><br /> |
<br /> | <br /> | ||
wobei <math>E: a_1x_1+a_2x_2+a_3x_3=b</math><br /> | wobei <math>E: a_1x_1+a_2x_2+a_3x_3=b</math><br /> | ||
Version vom 24. Januar 2013, 10:38 Uhr
Abstand zwischen Punkt und Gerade
1: Abstand mit Hilfe der Hilfsebene
Der Abstand zwischen Punkt A und Gerade g kann bestimmt werden, indem man eine sogenannte Hilfsebene senkrecht zur Geraden durch den Punkt A bildet.
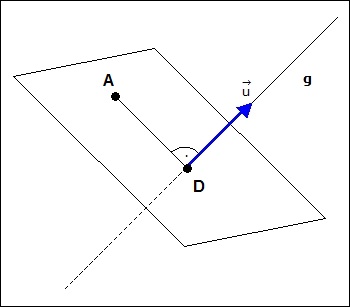
Um die Hilfsebene zu bilden, wird der Richtungsvektor 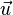 der Geraden g als Normalenvektor
der Geraden g als Normalenvektor 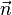 verwendet. Außerdem wird der Punkt A zur Bildung der Ebene für die Punktprobe eingesetzt. Im zweiten Schritt bestimmt man den Schnittpunkt D (Durchstoßpunkt)zwischen der Hilfsebene und der Geraden.
verwendet. Außerdem wird der Punkt A zur Bildung der Ebene für die Punktprobe eingesetzt. Im zweiten Schritt bestimmt man den Schnittpunkt D (Durchstoßpunkt)zwischen der Hilfsebene und der Geraden.
Als letztes entspricht der Abstand zwischen den Punkten A und D dem gesuchten Abstand zwischen Punkt und Gerade.
Bemerkung: Dies gilt auch für den Abstand zwischen parallelen Geraden in dem man die eine Gerade auf einen Stützvektor reduziert und die Hilfsebene senkrecht zum Stützvektor anlegt.
Kurz:
Geg: Punkt A; g; 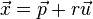
1.) Hilfsebene 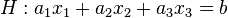
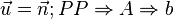
2.)Hilfsebene 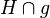
Schnittpunkt berechnen 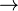 D
D
3.) 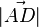 = gesuchter Abstand
= gesuchter Abstand
Beispiel:
geg: 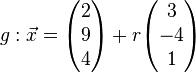
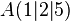
ges: Abstand zwischen Punkt und Gerade
1.) Hilfsebene
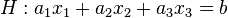
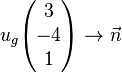 der Ebene
der Ebene
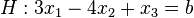
PP mit 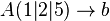
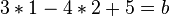
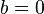
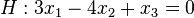
2.) Schnittpunkt D
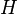 mit
mit 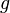 Schneiden
Schneiden 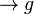 in
in 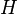
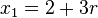
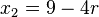
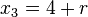
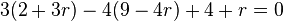
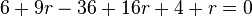
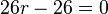
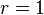
in 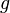 einsetzen
einsetzen
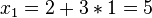
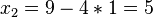
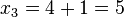
Daraus ergibt sich der Schnittpunkt 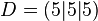
3.) 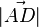 = gesuchter Abstand
= gesuchter Abstand
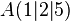
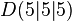
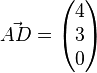
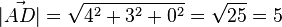
Bemerkung: Beim Abstand zwischen parallelen Geraden nimmt man von einer Geraden nur einen Punkt (Stützvektor) und bestimmt auf dieselbe Weise den Abstand.
2: Methode des laufenden Punktes
Mit der Methode des laufenden Punktes kann man den Abstand zwischen Punkt und Gerade oder zwischen zwei Geraden ebenfalls bestimmen. Diese Methode ist viel kürzer, da man hierbei den GTR verwenden kann. Man behandelt die Gerade als „laufenden Punkt“, das heißt man gibt ihn als Punkt in Abhängigkeit des Parameters an. Nun wird der Abstand des laufenden Punktes zu dem anderen festen Punkt bestimmt. Diese Wurzelfunktion (Zielfunktion) die sich dann im GTR zeichnen lässt, veranschaulicht alle Abstände zum festen Punkt. Daher ist die y-Koordinate des Tiefpunktes der kleinste Abstand. Die Stelle des Tiefpunktes (x-Wert) entspricht dem Parameter der Geraden. Setzt man ihn in die Gerade ein, erhält man den Punkt auf ihr, der den kleinsten Abstand zu dem festen Punkt hat.
Veranschaulichung anhand des letzten Beispiels:
geg: 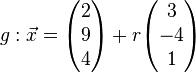
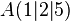
Alle Punkte auf g (laufender Punkt) lauten: 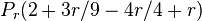
Der Vektor 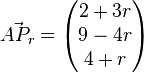
Die Länge des 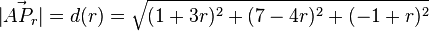
In diesem Fall ist 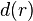 unsere Zielfunktion und nun sucht man mithilfe des GTR den Tiefpunkt der Funktion. Der GTR zeigt nämlich alle Abstände an und der Tiefpunkt ist der kürzeste.
unsere Zielfunktion und nun sucht man mithilfe des GTR den Tiefpunkt der Funktion. Der GTR zeigt nämlich alle Abstände an und der Tiefpunkt ist der kürzeste.
TP mit dem GTR ausrechnen und somit ist der 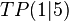 .
.
A: Der kürzeste Abstand ist 5.
Abstand zwischen einem Punkt und einer Ebene
Methode 1 mit Hilfe der Lotgeraden:
Hat man einen Punkt A und eine Ebene E im Raum, so lässt sich der Abstand mit Hilfe einer Lotgeraden bestimmten.
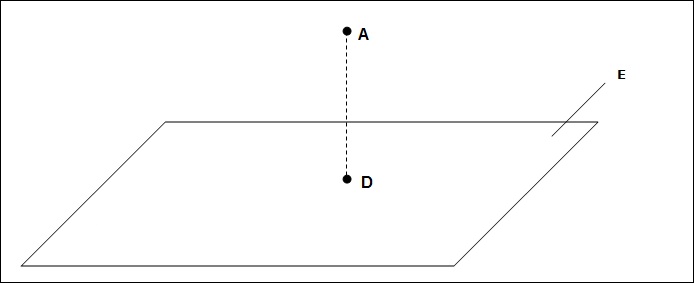
Schneidet man dann die Lotgerade mit der Ebene, erhält man den Durchstoßpunkt 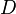 (Lotfußpunkt). Der Abstand zwischen den Punkten
(Lotfußpunkt). Der Abstand zwischen den Punkten 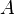 und
und 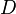 ist der Gesuchte Abstand.
ist der Gesuchte Abstand.
Kurz:
geg: Punkt A; E: 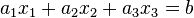
1.) Lotgerade bilden;
g: 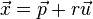
A ist der Stützvektor und 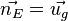
Das heißt, 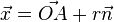
2.) Schnittpunkt bestimmen
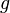 in
in 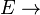 Durchstoßpunkt
Durchstoßpunkt 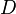
3.) 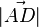 = gesuchter Abstand
= gesuchter Abstand
Beispiel:
geg: 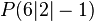
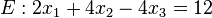
1.) Lotgerade bilden:
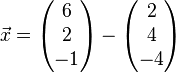
2.) Durchstoßpunkt D 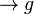 in
in 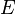 einsetzen
einsetzen
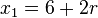
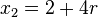
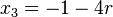
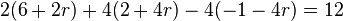
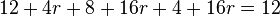
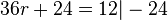
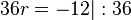
Fehler beim Parsen(Lexikalischer Fehler): r = -\frac{\12}{\36} = -\frac{\1}{\3}
Fehler beim Parsen(Lexikalischer Fehler): -\frac{\1}{\3}
ineinsetzen:
Fehler beim Parsen(Lexikalischer Fehler): x_1= 6-\frac{\2}{\3}= \frac{\16}{\3}
Fehler beim Parsen(Lexikalischer Fehler): x_2= 2-\frac{\4}{\3}= \frac{\2}{\3}
Fehler beim Parsen(Lexikalischer Fehler): x_3= -1+\frac{\4}{\3}= \frac{\1}{\3}
Fehler beim Parsen(Lexikalischer Fehler): D(\frac{\16}{\3}|\frac{\2}{\3}|\frac{\1}{\3})
3.)Fehler beim Parsen(Lexikalischer Fehler): \vec{AD} = \begin{pmatrix} -\frac{\2}{\3} \\ -\frac{\4}{\3} \\ \frac{\4}{\3}\end{pmatrix}
Fehler beim Parsen(Lexikalischer Fehler): \vec{\left| AD \right|}= \sqrt{(-\frac{\2}{\3})^2+(\frac{\4}{\3})^2+(\frac{\4}{\3})^2}
Fehler beim Parsen(Lexikalischer Fehler): \vec{\left| AD \right|}= \sqrt{\frac{\4}{\9}+\frac{\16}{\9}+\frac{\16}{\9}}
Fehler beim Parsen(Lexikalischer Fehler): \vec{\left| AD \right|}= \sqrt{\frac{\36}{\9}} = \sqrt{4} = 2
A: Der Abstand zwischen dem Punkt 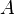 und der Ebene
und der Ebene 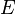 ist 2.
ist 2.
Methode 2 mit Hilfe der Hesse'sche Normalenform:
Basierend auf der Hesse’schen Normalenform HNF lässt sich der Abstand eines Punktes und einer Ebene berechnen mit:
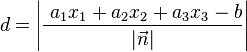
wobei 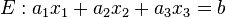
Setzt man den Punkt 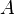 in den Zähler, erhält man den gesuchten Abstand
in den Zähler, erhält man den gesuchten Abstand 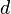 .
.
Beispiel:
geg: 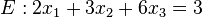
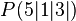
ges: Abstand zwischen 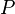 und
und 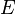
HNF von E: Fehler beim Parsen(Syntaxfehler): \frac{\| 2x_1-3x_2+6x_3-3 |}{\sqrt{2^2+(-3)^2+(6)^2}
Fehler beim Parsen(Lexikalischer Fehler): \frac{\left| 2x_1-3x_2+6x_3-3 \right|}{\7}
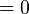
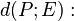 Fehler beim Parsen(Lexikalischer Fehler): \frac{| 2*5+3*1+6*3-3| }{\7}=\frac{\left| 28 \right|}{\7} = \frac{28}{\7} = 4
Fehler beim Parsen(Lexikalischer Fehler): \frac{| 2*5+3*1+6*3-3| }{\7}=\frac{\left| 28 \right|}{\7} = \frac{28}{\7} = 4
Bemerkung: Dieses Verfahren wendet man auch beim Abstand zwischen parallelen Geraden – Ebenen oder Ebenen – Ebenen an, indem die Gerade oder die eine Ebene auf einen Punkt reduziert wird. Den Stützvektor bei Geraden oder Spurpunkt bei Ebenen.

