Extremwertprobleme: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „= Extremwertprobleme = Extremwertprobleme sind Aufgaben, bei denen etwas (zum Beispiel eine Fläche) unter bestimmten Bedingungen minimiert oder maximiert we…“) |
(→Schritt 5) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
| − | + | == Beispielaufgabe == | |
| Zeile 21: | Zeile 21: | ||
Die Zielfunktion ist der mathematische Term, der das beschreibt, was man letztlich minimieren/maximieren will. | Die Zielfunktion ist der mathematische Term, der das beschreibt, was man letztlich minimieren/maximieren will. | ||
| − | Um einen möglichst großen Stall zu erhalten, muss die Fläche A so groß wie möglich sein, also: A = a * b | + | Um einen möglichst großen Stall zu erhalten, muss die Fläche A so groß wie möglich sein, also: A = a * b<br /> |
a ist dabei die eine Seite des Rechtecks, b die andere Seite. | a ist dabei die eine Seite des Rechtecks, b die andere Seite. | ||
| Zeile 73: | Zeile 73: | ||
== Schritt 5 == | == Schritt 5 == | ||
| − | '''Weitere Nebenbedingungen überprüfen, zweite Größe berechnen und Aufgabe sinnvoll beantworten.'''<br /> | + | '''Weitere Nebenbedingungen überprüfen, zweite Größe berechnen und Aufgabe sinnvoll beantworten. Wichtig dabei: Einheiten beachten!'''<br /> |
| + | |||
| + | |||
2 = 2 * (a + b)<br /> | 2 = 2 * (a + b)<br /> | ||
| − | 2 = 2 * (a + 0.5) | + | 2 = 2 * (a + 0.5) <br /> |
| − | 1 = a + 0.5 | + | 1 = a + 0.5 <br /> |
0.5 = a | 0.5 = a | ||
| Zeile 88: | Zeile 90: | ||
Somit muss der Hasenstall muss eine Breite von 0.5m und eine Länge von 0.5m haben. | Somit muss der Hasenstall muss eine Breite von 0.5m und eine Länge von 0.5m haben. | ||
| − | + | == Aufgaben mit Lösungen und Rechenweg == | |
| − | Eine Getränkefirma will eine neue Getränkedose designen. Sie will dafür pro Dose 0.3 m² Blech benutzen. Der Einfachheit halber wird angenommen, die Dose sei ein Zylinder. Wie muss die Dose gebaut sein, dass möglichst viel Inhalt hineinpasst? | + | Eine Getränkefirma will eine neue Getränkedose designen. Sie will dafür pro Dose 0.3 m² Blech benutzen. Der Einfachheit halber wird angenommen, die Dose sei ein Zylinder. Wie muss die Dose gebaut sein, dass möglichst viel Inhalt hineinpasst? (Hilfsmittel: Taschenrechner) |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| Zeile 99: | Zeile 101: | ||
Nebenbedingung: Die Wand + Boden + Deckel sind 0.3 m² groß:<br /> | Nebenbedingung: Die Wand + Boden + Deckel sind 0.3 m² groß:<br /> | ||
| − | 0.3 = A + A + h * U<br /> | + | <math>0.3 = A + A + h * U</math><br /> |
| − | 0.3 = 2A + h * U<br /> | + | <math>0.3 = 2A + h * U</math><br /> |
| − | 0.3 = | + | <math>0.3 = 2 \pi r^2 + h * 2 \pi r</math><br /> |
| − | 0.3 = | + | <math>0.3 = 2 \pi r * (r + h)</math><br /> |
| − | 0.3 | + | |
| − | + | <math>\frac{0.3}{2\pi r} = r + h</math><br /> | |
| + | |||
| + | <math>\frac{0.3}{2\pi r} - r = h</math><br /> | ||
Einsetzen in V: <br /> | Einsetzen in V: <br /> | ||
| − | V(r) = | + | |
| − | V(r) = | + | <math>V(r) = \pi * r^2 * (\frac{0.3}{2\pi r} - r)</math><br /> |
| − | V(r) = 0.15r - | + | |
| + | <math>V(r) = \frac{0.3 * \pi * r^2}{2\pi r} - \pi r^3</math><br /> | ||
| + | |||
| + | <math>V(r) = 0.15r - \pi r^3</math><br /> | ||
Desweiteren dürfen weder h noch r negativ sein. | Desweiteren dürfen weder h noch r negativ sein. | ||
Maximum mit V'(r) finden:<br /> | Maximum mit V'(r) finden:<br /> | ||
| − | -> Maximum bei r = <math>\sqrt{\frac{0.05}{ | + | -> Maximum bei r = <math>\sqrt{ \frac{0.05}{\pi} } = \pm 0.126 </math> (Mit Taschenrechner)<br /> |
Allerdings ist nur die positive Lösung r = 0.126 zulässig.<br /> | Allerdings ist nur die positive Lösung r = 0.126 zulässig.<br /> | ||
| Zeile 123: | Zeile 130: | ||
Die Dose muss also eine Höhe von 0.253 m haben und ihre kreisförmige Grundfläche einen Radius von 0.126 m. | Die Dose muss also eine Höhe von 0.253 m haben und ihre kreisförmige Grundfläche einen Radius von 0.126 m. | ||
| + | </popup> | ||
| + | |||
| + | Ein Bauer will einen rechteckigen Hühnerstall an einer Mauer anbauen (Eine Seite des Rechtecks muss also nicht mehr gebaut werden). Er hat dafür 20m Maschendraht zur Verfügung. Wie muss er den Stall anlegen, sodass die Hühner möglichst viel Platz haben? (Ohne Hilfsmittel) | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | |||
| + | Die zu maximierende Zielfunktion ist der Flächeninhalt des Rechtecks: <br /> | ||
| + | A = a * b.<br /> | ||
| + | <br /> | ||
| + | Die Nebenbedingung ist dabei: 20 = a + a + b (Nur einmal "b", da eine Seite ja bereits durch die Mauer ersetzt wird.)<br /> | ||
| + | 20 = 2 * a + b<br /> | ||
| + | 20 - 2a = b<br /> | ||
| + | <br /> | ||
| + | Einsetzen in die Zielfunktion: <br /> | ||
| + | A(a) = a * (20 - 2a)<br /> | ||
| + | A(a) = 20a - 2a²<br /> | ||
| + | Maximum bestimmen mit A'(a)<br /> | ||
| + | -> Maximum bei a = 5<br /> | ||
| + | <br /> | ||
| + | "b" berechnen: <br /> | ||
| + | b = 20 - 2a<br /> | ||
| + | b = 20 - 10<br /> | ||
| + | b = 10<br /> | ||
| + | <br /> | ||
| + | Der Zaun muss so aufgestellt werden, dass zwei Seiten 5m lang sind und die eine, der Mauer gegenüberliegende, Seite 10m lang ist. | ||
</popup> | </popup> | ||
Aktuelle Version vom 2. März 2018, 00:12 Uhr
Inhaltsverzeichnis |
Extremwertprobleme
Extremwertprobleme sind Aufgaben, bei denen etwas (zum Beispiel eine Fläche) unter bestimmten Bedingungen minimiert oder maximiert werden soll, also den größten oder kleinsten Wert gefunden werden soll, bei dem dennoch alle Nebenbedingungen zutreffen.
Beispielaufgabe
Tim will einen möglichst großen, aber rechteckigen Hasenstall bauen. Dazu will er im Baumarkt eine Umzäunung der Länge 2m kaufen. Wie muss er den Stall aufbauen?
Anhand dieser Beispielaufgabe wird im Folgenden die Lösung von Extremwertproblemen behandelt.
Schritt 1
Zielfunktion finden und aufstellen.
Die Zielfunktion ist der mathematische Term, der das beschreibt, was man letztlich minimieren/maximieren will.
Um einen möglichst großen Stall zu erhalten, muss die Fläche A so groß wie möglich sein, also: A = a * b
a ist dabei die eine Seite des Rechtecks, b die andere Seite.
Schritt 2
Alle weiteren Informationen herausarbeiten und in Nebenbedingungen formulieren.
Nebenbedingungen sind die Bedingungen, die in jedem Fall gelten müssen. Dazu gehören auch Wertebereiche, die zwar nicht unbedingt aufgeschrieben, aber trotzdem im
Hinterkopf behalten und später überprüft werden müssen.
In diesem Beispiel: da die gesamte Umzäunung 2m Länge hat, entspricht dies dem Umfang:
U = 2 = a + a + b + b = 2 * (a + b)
2 = 2 * (a + b)
Außerdem sollte klar sein, dass weder a noch b negativ oder 0 sein können, aber auch nicht länger als 2m sind: 0 < a < 2 und 0 < b < 2
Schritt 3
Umformen und Einsetzen.
2 = 2 * (a + b)
1 = a + b
a = 1 – b
Einsetzen in A: A = (1 – b) * b = b – b²
Da die Fläche A ist nun nur noch abhängig von b. Man kann also auch schreiben: A(b) = b – b²
Schritt 4
Gesuchtes Extremum finden.
Da in der Aufgabe nach einer möglichst großen Fläche gefragt ist, wird als das Maximum bestimmt.
A(b) = b – b²
Maximum mit der Ableitung A'(b) herausfinden.
-> Maximum bei b = 0.5
Schritt 5
Weitere Nebenbedingungen überprüfen, zweite Größe berechnen und Aufgabe sinnvoll beantworten. Wichtig dabei: Einheiten beachten!
2 = 2 * (a + b)
2 = 2 * (a + 0.5)
1 = a + 0.5
0.5 = a
Sowohl a und b entsprechen dem Wertebereich von 0 < a < 2 und 0 < b < 2.
Somit muss der Hasenstall muss eine Breite von 0.5m und eine Länge von 0.5m haben.
Aufgaben mit Lösungen und Rechenweg
Eine Getränkefirma will eine neue Getränkedose designen. Sie will dafür pro Dose 0.3 m² Blech benutzen. Der Einfachheit halber wird angenommen, die Dose sei ein Zylinder. Wie muss die Dose gebaut sein, dass möglichst viel Inhalt hineinpasst? (Hilfsmittel: Taschenrechner)
Ein Bauer will einen rechteckigen Hühnerstall an einer Mauer anbauen (Eine Seite des Rechtecks muss also nicht mehr gebaut werden). Er hat dafür 20m Maschendraht zur Verfügung. Wie muss er den Stall anlegen, sodass die Hühner möglichst viel Platz haben? (Ohne Hilfsmittel)
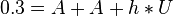
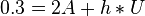
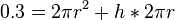
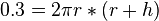
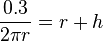
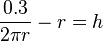
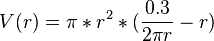
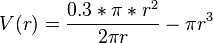
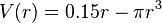
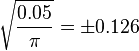 (Mit Taschenrechner)
(Mit Taschenrechner)
