Die Stammfunktion: Unterschied zwischen den Versionen
(→Graph der Stammfunktion) |
|||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 67: | Zeile 67: | ||
Allgemeine Form: | Allgemeine Form: | ||
<br \> | <br \> | ||
| − | <math>f(x)= | + | <math>f(x)=u(v(x))</math><br \> |
<br \> | <br \> | ||
| − | <math>F(x)=\int f (x)\,dx ={\int | + | <math>F(x)=\int f (x)\,dx ={\int u(v(x))\,dx \over{v'(x)}}</math><br \> |
In Worten: Um bei einer Verkettung von Funktionen an die Stammfunktion zu kommen muss man das Integral der äußeren Funktion durch die Ableitung der inneren Funktion teilen. | In Worten: Um bei einer Verkettung von Funktionen an die Stammfunktion zu kommen muss man das Integral der äußeren Funktion durch die Ableitung der inneren Funktion teilen. | ||
Beispiel:<br \> | Beispiel:<br \> | ||
<math>f(x)=(2x-5)^2</math><br \> | <math>f(x)=(2x-5)^2</math><br \> | ||
| − | <math> | + | <math>u(v(x))=()^2 -> \int u (v(x))\,dx ={1 \over3}()^3</math><br \> |
| − | <math> | + | <math>v(x)=2x-5 -> v'(x)=2</math><br \> |
also:<math>F(x)={{1 \over3}(2x-5)^3 \over2}+c</math> | also:<math>F(x)={{1 \over3}(2x-5)^3 \over2}+c</math> | ||
| − | |||
==== Faktorregel ==== | ==== Faktorregel ==== | ||
| Zeile 106: | Zeile 105: | ||
[[Datei:Stammfunktionen1.jpg]] | [[Datei:Stammfunktionen1.jpg]] | ||
| − | + | ||
| + | === Herleitung und Beweiß des "+C" === | ||
| + | |||
| + | Die Funktion <math>F(x)</math> ist die Stammfunktion der Funktion <math>f(x)</math>. <br \> | ||
| + | Nun hat die Funktion <math>f(x)</math> nicht nur eine Stammfunktion, sondern unendlich viele. Beispielsweise gilt auch <math>F(x)=K(x)+c</math>. <br \> | ||
| + | <math>c</math> ist eine Konstante für die eine beliebige Zahl eingesetzt werden kann.<br \> | ||
| + | Beweis:<br \> | ||
| + | Wenn für die Stammfunktion <math>F(x)</math> gilt, dass <math>F'(x)=f(x)</math>, so muss auch für <math>K</math> <math>K'(x)=f(x)</math> gelten.<br \> | ||
| + | Es muss also gelten, dass <math>F'(x)-K'(x)=0</math>, da nach der Summenregel vom Ableiten gilt, dass ein Summand beim Ableiten wegfällt. Das "<math>+C</math>" fällt also weg und so haben <math>K</math> und <math>F</math>, für gleiches <math>x</math>, auch den selben Betrag.<br \> | ||
| + | <math>F-K</math> ist eine konstante Funktion, da sich <math>F</math> und <math>K</math> nur durch <math>c</math> unterscheiden.<br \> | ||
| + | Es gilt:<br \> | ||
| + | <math>F(x)-K(x)=c</math>, nach <math>F(x)</math> umgeformt: <math>F(x)=K(x)+c</math> <br \> | ||
| + | <br \> | ||
| + | Also hat jede Funktion <math>f</math> unendlich viele Stammfunktionen. | ||
Aktuelle Version vom 3. Dezember 2012, 19:07 Uhr
Inhaltsverzeichnis |
Definition der Stammfunktion
Die Funktion 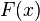 der Ausgangsfunktion
der Ausgangsfunktion  heißt Stammfunktion.
heißt Stammfunktion. 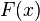 ist die differenzierbare Funktion der reellen Funktion
ist die differenzierbare Funktion der reellen Funktion  , sodass gilt:
, sodass gilt:
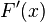


Jede Funktion  hat unendlich viele Stammfunktionen.
hat unendlich viele Stammfunktionen.
Auf die Stammfunktion kommt man, indem man die Ausgangsfunktion integriert, also:
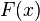

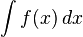
Stammfunktionen zu einfachen Funktionen
 |
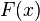
|
|---|---|
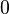 |

|
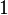 |
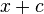
|
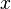 |
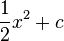
|
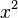 |
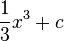
|
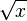  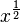 |
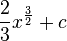
|
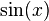 |
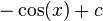
|
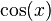 |
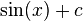
|
Integrationsregeln zum Berechnen der Stammfunktion
Um an die Stammfunktion zu kommen muss man die Funktion  integrieren. Dabei muss man bestimmte Regeln beachten von denen manche den bereits bekannten Ableitungsregeln ähnlich sind.
integrieren. Dabei muss man bestimmte Regeln beachten von denen manche den bereits bekannten Ableitungsregeln ähnlich sind.
Potenzregel
Möchte man eine Potenzfunktion wie zum Beispiel 

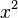 integrieren um an die Stammfunktion zu kommen, so gilt:
integrieren um an die Stammfunktion zu kommen, so gilt:
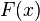

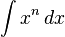

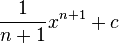
Beispiel: 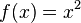
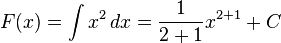

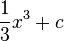
Summenregel
Möchte man eine Summe von zwei Funktionen integrieren so gilt die selbe Regel, wie beim Ableiten:
Summenregel beim Ableiten:
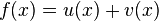
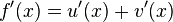
Genau wie beim Ableiten werden beim Integrieren die Summanden einzeln integriert und dann stehen gelassen oder vereinfacht.
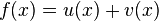
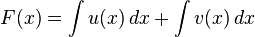
Kettenregel
Möchte man eine Verkettung von Funktionen Integrieren, um an die Stammfunktion zu gelangen, so muss man die Kettenregel vom Integrieren benutzen. Diese ähnelt der Kettenregel beim Ableiten, ist jedoch nicht die selbe:
Die folgende Regel gilt nur bei linearer Verkettung, das heißt, dass es sich bei der "inneren" Funktion um eine lineare Funktion handeln muss!
Allgemeine Form:
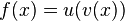
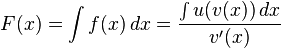
In Worten: Um bei einer Verkettung von Funktionen an die Stammfunktion zu kommen muss man das Integral der äußeren Funktion durch die Ableitung der inneren Funktion teilen.
Beispiel:
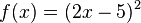
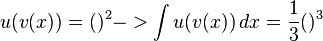
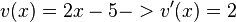
also: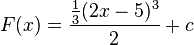
Faktorregel
Für Produkte aus einem bestimmten Faktor und einer Funktion:
Der Faktor bleibt stehen und die Funktion wird Integriert.(Analog zum Ableiten)
Beispiel:
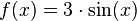
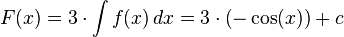
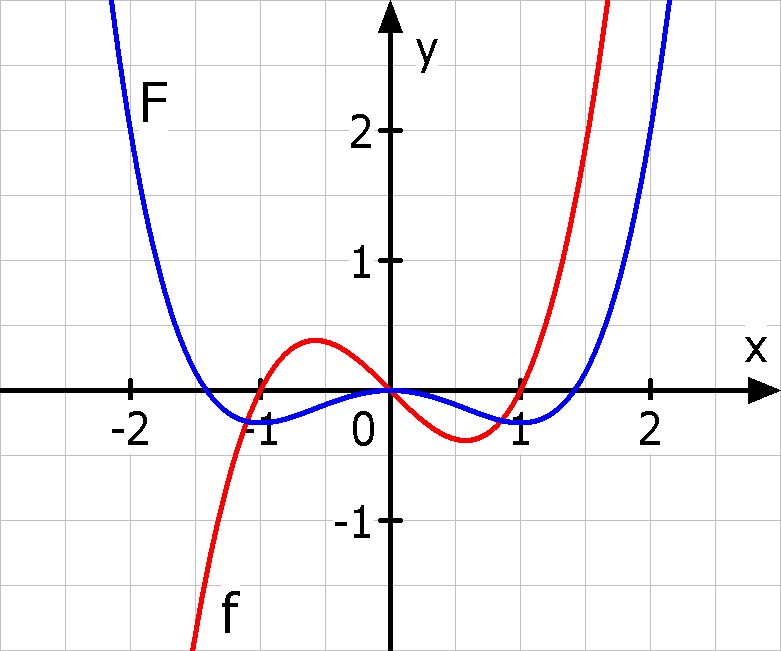
Graph der Stammfunktion
Anhand bestimmter Stellen des Graphen der Funktion  kann man, den Graphen der Stammfunktion
kann man, den Graphen der Stammfunktion 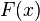 skizzieren.
skizzieren.
Dabei gilt:
1. An der Stelle (a), wo der Graph von  eine Nullstelle hat, muss der Graph der Stammfunktion einen Extrempunkt mit waagerechter Tangente haben.
eine Nullstelle hat, muss der Graph der Stammfunktion einen Extrempunkt mit waagerechter Tangente haben.
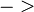 es gilt:
es gilt: 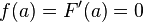
(Vergleich Ausgangsfunktion mit erster Ableitung)
2.An der Stelle (b), wo der Graph von  eine Extremstelle hat, muss der Graph der Stammfunktion eine Wendestelle haben.
eine Extremstelle hat, muss der Graph der Stammfunktion eine Wendestelle haben.
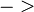 es gilt:
es gilt: 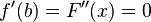
Außerdem muss der Graph der Stammfunktion an Stelle b eine Wendestelle haben, es bei einem Hoch-oder Tiefpunkt immer einen Vorzeichenwechsel vom Positiven ins Negative oder umgekehrt gibt.
(Vergleich erste Ableitung mit zweiter Ableitung)
3. Gilt bei der Funktion  in einem festgelegten Intervall
in einem festgelegten Intervall 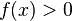 , so ist der Graph der Stammfunktion in diesem Intervall streng monoton steigend. Gilt
, so ist der Graph der Stammfunktion in diesem Intervall streng monoton steigend. Gilt 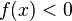 , so ist der Graph der Stammfunktion in diesem Intervall streng monoton fallend.
, so ist der Graph der Stammfunktion in diesem Intervall streng monoton fallend.
Herleitung und Beweiß des "+C"
Die Funktion 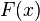 ist die Stammfunktion der Funktion
ist die Stammfunktion der Funktion  .
.
Nun hat die Funktion  nicht nur eine Stammfunktion, sondern unendlich viele. Beispielsweise gilt auch
nicht nur eine Stammfunktion, sondern unendlich viele. Beispielsweise gilt auch 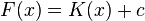 .
.
 ist eine Konstante für die eine beliebige Zahl eingesetzt werden kann.
ist eine Konstante für die eine beliebige Zahl eingesetzt werden kann.
Beweis:
Wenn für die Stammfunktion 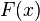 gilt, dass
gilt, dass 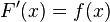 , so muss auch für
, so muss auch für 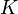
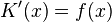 gelten.
gelten.
Es muss also gelten, dass 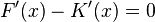 , da nach der Summenregel vom Ableiten gilt, dass ein Summand beim Ableiten wegfällt. Das "
, da nach der Summenregel vom Ableiten gilt, dass ein Summand beim Ableiten wegfällt. Das "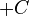 " fällt also weg und so haben
" fällt also weg und so haben 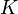 und
und 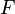 , für gleiches
, für gleiches 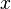 , auch den selben Betrag.
, auch den selben Betrag.
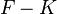 ist eine konstante Funktion, da sich
ist eine konstante Funktion, da sich 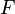 und
und 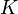 nur durch
nur durch  unterscheiden.
unterscheiden.
Es gilt:
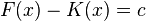 , nach
, nach 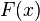 umgeformt:
umgeformt: 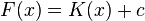
Also hat jede Funktion 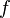 unendlich viele Stammfunktionen.
unendlich viele Stammfunktionen.