Geradlinige Bewegung: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Formeln einer gleichförmigen Bewegung)
(→‎Anwendungsbeispiele gleichförmiger Bewegungen)
 
(23 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Man kann diese Bewegung in zwei Kategorien einteilen:
+
Geradlinige Bewegungen sind Bewegungen die unabhänig von ihrer Geschwindigkeit und Beschleunigung ihre Richtung beibehalten. Man kann diese Bewegung in zwei Kategorien einteilen:
  
 +
* Gleichförmige Bewegung(Bewegung mit konstanter Geschwindigkeit)
  
−
* Bewegung mit konstanter Geschwindigkeit
+
* Beschleunigte Bewegungen
 +
:* Gleichmäßige Beschleunigung (Freier Fall als Sonderfall)
 +
:*
  
−
 
−
* Beschleunigte Bewegungen darunter fällt:
 
−
    *gleichmäßig Beschleunigung
 
−
    *
 
  
 
== geradlinig gleichförmige Bewegung ==
 
== geradlinig gleichförmige Bewegung ==
 +
 +
Geradlinige gleichförmige Bewegungen gibt es, wenn sich ein Körper mit einer konstanten Geschwindigkeit bewegt. Aus den Werten ergibt sich im s/t Diagramm eine Gerade, welche man mit einer liniaren Funktion beschreiben kann.
  
 
=== Diagramme einer gleichförmigen Bewegung ===
 
=== Diagramme einer gleichförmigen Bewegung ===
 +
 +
in Bearbeitung
  
 
=== Formeln einer gleichförmigen Bewegung ===
 
=== Formeln einer gleichförmigen Bewegung ===
−
Ein Fahrzeug mit gleichbleibender Geschwindigkeit bewegt sich pro Zeiteinheit immer um die selbe Strecke fort.
+
Ein Fahrzeug mit gleichbleibender Geschwindigkeit bewegt sich pro Zeitintervall immer um dieselbe Strecke fort.
 
Deshalb gilt die allgemeine Formel:
 
Deshalb gilt die allgemeine Formel:
  
−
v=s/t
+
<math>v= {\Delta s \over \Delta t} </math>
  
 
Durch einfaches mathematisches Umstellen kann man sich so auch die Formeln für die Strecke und die Zeit bei konstanter Geschwindigkeit herleiten.
 
Durch einfaches mathematisches Umstellen kann man sich so auch die Formeln für die Strecke und die Zeit bei konstanter Geschwindigkeit herleiten.
  
−
v=s/t               |*t
+
<math>v= {s \over t}  \quad \qquad | \cdot t</math>
  
−
s=v*t               |/v
+
<math>s = v \cdot t \qquad  | :v </math>
  
−
t=s/v
+
<math>t = {s \over v} </math>
  
 
=== Anwendungsbeispiele gleichförmiger Bewegungen ===
 
=== Anwendungsbeispiele gleichförmiger Bewegungen ===
  
 
Ein Fahrrad bewegt sich mit konstanter Geschwindigkeit um eine Strecke von 16m.
 
Ein Fahrrad bewegt sich mit konstanter Geschwindigkeit um eine Strecke von 16m.
 +
Alle zwei Meter wird eine Zeitmessung unternommen und die Werte aufgeschrieben.
 +
 +
 +
{| border="1"
 +
|Strecke: 
 +
|s in m
 +
|0
 +
|2
 +
|4
 +
|6
 +
|8 
 +
|10
 +
|12
 +
|14
 +
|16
 +
|-
 +
|Lauf 1:
 +
|t in s
 +
|0
 +
| 0,38
 +
|  0,98
 +
| 1,29
 +
| 1,78
 +
| 2,3
 +
|  2,61
 +
|  3,18
 +
|  3,98
 +
|-
 +
|Lauf 2:
 +
|    t in s
 +
| 0
 +
| 0,74
 +
|  1,56
 +
| 2,22
 +
| 3,06
 +
| 3,99
 +
|  4,46
 +
|  5,0
 +
|  6,64
 +
|}
 +
 +
Bestimme die Steigung der Graphen und damit die Geschwindigkeit.
 +
 +
{{Lösung versteckt|
 +
1=V<small>lauf1</small>=4,5m/s  V<small>lauf2</small>=2,5m/s
 +
}}
 +
 +
 +
Eine Schnecke sieht sieht in eriner Entfernung von 90m eine Kneipe. Mit einer Geschwindigkeit von 0,5cm/s läuft sie los. Wie lange dauert die Reise?
 +
 +
 +
 +
{{Lösung versteckt| 1=
 +
 +
Geg: s=90m=9000cm      v=0,5cm/s
 +
Ges: t
 +
Lös:
 +
 +
t=s/v    -->    9000cm/0,5cm/s = 18000s = 300min = 5h
 +
}}
  
 
== geradlinig gleichmäßig beschleunigte Bewegung ==
 
== geradlinig gleichmäßig beschleunigte Bewegung ==
Zeile 41: Zeile 104:
 
<math>s = {1 \over 2} \cdot a \cdot t^2 </math>
 
<math>s = {1 \over 2} \cdot a \cdot t^2 </math>
  
−
<math> \vec a = \lim_{\triangle t\to 0} {\triangle \vec v \over \triangle t }</math>
+
<math>s = {{1 \over 2} \cdot v \cdot t}</math>
  
−
<math>v = a \cdot t</math>
+
<math>a = {v \over t}</math>
  
 
=== Anwendungsbeispiele beschleunigter Bewegungen ===
 
=== Anwendungsbeispiele beschleunigter Bewegungen ===
  
−
=== Freier Fall ===
+
=== freier Fall ===
 +
Beispiele für freier Fall:
 +
 
 +
3 Körper unterschiedlicher Masse werden von eine hohen Punkt fallen gelassen (Vakuum). Welcher Körper kommt zuerst unten an?
 +
 
 +
 
 +
 
 +
 
 +
* Es ist anzunehmen, dass die schwereren Körper schneller fallen.
 +
* Daraus folgern wir, dass Körper 1 schneller als 2 und 3 ist und demnach 2 schneller als 3.
 +
* Dies kann aber nicht stimmen, da bei Körper 1 der kleinere den größeren ausbremsen muss(Körper 1 ist deshalb langsamer als Körper 2).
 +
* Somit ist unsere erste Annahme '''falsch''' !
 +
* Wir schließen daraus, dass alle Körper gleich schnell fallen müssen und somit ihre Fallgeschwindigkeit nichts mit der Masse zu tun  hat. Denn sie werden ständig beschleunigt und somit steigt auch ihre Geschwindigkeit ständig an.

Aktuelle Version vom 11. Dezember 2012, 21:57 Uhr

Geradlinige Bewegungen sind Bewegungen die unabhänig von ihrer Geschwindigkeit und Beschleunigung ihre Richtung beibehalten. Man kann diese Bewegung in zwei Kategorien einteilen:

  • Gleichförmige Bewegung(Bewegung mit konstanter Geschwindigkeit)
  • Beschleunigte Bewegungen
  • Gleichmäßige Beschleunigung (Freier Fall als Sonderfall)


Inhaltsverzeichnis

geradlinig gleichförmige Bewegung

Geradlinige gleichförmige Bewegungen gibt es, wenn sich ein Körper mit einer konstanten Geschwindigkeit bewegt. Aus den Werten ergibt sich im s/t Diagramm eine Gerade, welche man mit einer liniaren Funktion beschreiben kann.

Diagramme einer gleichförmigen Bewegung

in Bearbeitung

Formeln einer gleichförmigen Bewegung

Ein Fahrzeug mit gleichbleibender Geschwindigkeit bewegt sich pro Zeitintervall immer um dieselbe Strecke fort. Deshalb gilt die allgemeine Formel:

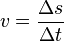
v= {\Delta s \over \Delta t}

Durch einfaches mathematisches Umstellen kann man sich so auch die Formeln für die Strecke und die Zeit bei konstanter Geschwindigkeit herleiten.

v= {s \over t} \quad \qquad | \cdot t

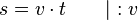
s = v \cdot t \qquad | :v

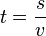
t = {s \over v}

Anwendungsbeispiele gleichförmiger Bewegungen

Ein Fahrrad bewegt sich mit konstanter Geschwindigkeit um eine Strecke von 16m. Alle zwei Meter wird eine Zeitmessung unternommen und die Werte aufgeschrieben.


Strecke: s in m 0 2 4 6 8 10 12 14 16
Lauf 1: t in s 0 0,38 0,98 1,29 1,78 2,3 2,61 3,18 3,98
Lauf 2: t in s 0 0,74 1,56 2,22 3,06 3,99 4,46 5,0 6,64

Bestimme die Steigung der Graphen und damit die Geschwindigkeit.

Vlauf1=4,5m/s Vlauf2=2,5m/s


Eine Schnecke sieht sieht in eriner Entfernung von 90m eine Kneipe. Mit einer Geschwindigkeit von 0,5cm/s läuft sie los. Wie lange dauert die Reise?


Geg: s=90m=9000cm v=0,5cm/s Ges: t Lös:

t=s/v --> 9000cm/0,5cm/s = 18000s = 300min = 5h


geradlinig gleichmäßig beschleunigte Bewegung

Diagramme einer gleichmäßig beschleunigten Bewegung

in Bearbeitung

Formeln einer gleichmäßig beschleunigten Bewegung

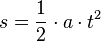
s = {1 \over 2} \cdot a \cdot t^2

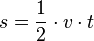
s = {{1 \over 2} \cdot v \cdot t}

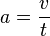
a = {v \over t}

Anwendungsbeispiele beschleunigter Bewegungen

freier Fall

Beispiele für freier Fall:

3 Körper unterschiedlicher Masse werden von eine hohen Punkt fallen gelassen (Vakuum). Welcher Körper kommt zuerst unten an?



  • Es ist anzunehmen, dass die schwereren Körper schneller fallen.
  • Daraus folgern wir, dass Körper 1 schneller als 2 und 3 ist und demnach 2 schneller als 3.
  • Dies kann aber nicht stimmen, da bei Körper 1 der kleinere den größeren ausbremsen muss(Körper 1 ist deshalb langsamer als Körper 2).
  • Somit ist unsere erste Annahme falsch !
  • Wir schließen daraus, dass alle Körper gleich schnell fallen müssen und somit ihre Fallgeschwindigkeit nichts mit der Masse zu tun hat. Denn sie werden ständig beschleunigt und somit steigt auch ihre Geschwindigkeit ständig an.
Von „http://fsg.zum.de/index.php?title=Geradlinige_Bewegung&oldid=913“