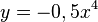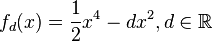Funktionenscharen: Unterschied zwischen den Versionen
(→Funktionenscharen) |
(→Ortskurven) |
||
| Zeile 60: | Zeile 60: | ||
'''Bestimmen von Ortskurven''' | '''Bestimmen von Ortskurven''' | ||
| − | Die Koordinaten des Extrempunktes sind <math> E_1 ( 0 | 0 ) </math>, <math> E_2 ( sqrt d | - 0,5 d^2) </math>, <math> E_3 ( -sqrt d | - 0,5 d^2) </math> | + | Die Koordinaten des Extrempunktes sind <math> E_1 ( 0 | 0 ) </math>, <math> E_2 ( \sqrt d | - 0,5 d^2) </math>, <math> E_3 ( -\sqrt d | - 0,5 d^2) </math> |
| Zeile 67: | Zeile 67: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | x&=sqrt d \\ | + | x&=\sqrt d \\ |
| − | y&= f( sqrt d ) = - 0,5 d^2 | + | y&= f( \sqrt d ) = - 0,5 d^2 |
\end{align} | \end{align} | ||
</math> | </math> | ||
Version vom 21. Februar 2014, 09:42 Uhr
Die folgenden Kapitel werden anhand einer Aufgabe erklärt.
30px Aufgabe
Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte? |
Funktionenscharen
Berechnung der Extrempunkte:
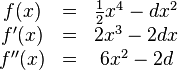
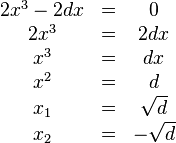
→ d kann nicht negativ werden
Vorsicht - hier ist ein Fehler. Es gibt drei Lösungen, nicht nur eine! [Btm]
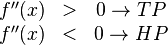
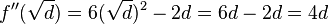
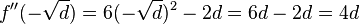
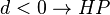
Vorsicht: Kann 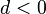 nun doch gelten? [Btm]
nun doch gelten? [Btm]
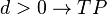
Ortskurven
Bestimmung der Ortskurve der Hochpunkte:
Ortskurven sind Kurven, auf denen Punkte mit gleichen Eigenschaften einer Kurvenschar liegen z.B alle Hochpunkte.
Bestimmen von Ortskurven
Die Koordinaten des Extrempunktes sind 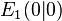 ,
, 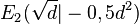 ,
, 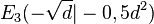
Koordinaten der Extrempunkte einzeln aufschreiben:
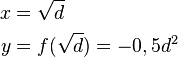
x - Koordinate nach Parameter auflösen:
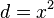
Diesen Parameter in die y - Gleichung einsetzen:
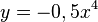
Gleichung der Ortskurve der Extrempunkte: