Beschränktes Wachstum: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(Die Seite wurde neu angelegt: „Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (po…“) |
|||
| Zeile 4: | Zeile 4: | ||
<math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br /> | <math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br /> | ||
<math>{S}</math> steht für die Schranke die nicht überschritten werden kann. <br /> | <math>{S}</math> steht für die Schranke die nicht überschritten werden kann. <br /> | ||
| − | <math>{a}</math> steht für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{x=0}</math> .<br /> | + | <math>{a}</math> steht für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{x=0}</math> . Zudem bestimmt das Vorzeichen vor dem <math>{a}</math>, ob das Wachstum nach oben oder nach unten begrenzt ist.<br /> |
| − | <math>{k}</math> steht für die Wachstums- | + | <math>{k}</math> steht für die Wachstumskonstante. |
| + | ===Differenzialgleichung=== | ||
| + | Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums<br /> | ||
| + | <math>{f'(x)=k \cdot (S-f(x))}</math>.<br /><br /> | ||
| + | Erklärung:<br /> | ||
| + | Die Differenzialgleichung ausgeschrieben lautet:<br /> | ||
| + | <math>{f'(x)=k \cdot (S-(S-a \cdot e^{-k \cdot x}))}</math><br /> | ||
| + | Vereinfacht:<br /> | ||
| + | <math>{f'(x)=k \cdot a \cdot e^{-k \cdot x}}</math><br /> | ||
Version vom 4. September 2018, 12:14 Uhr
Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.
Funktionsgleichun
Funktionsterm
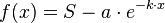
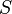 steht für die Schranke die nicht überschritten werden kann.
steht für die Schranke die nicht überschritten werden kann.
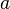 steht für den Anfangsbestand, also den Bestand zum Zeitpunkt
steht für den Anfangsbestand, also den Bestand zum Zeitpunkt 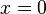 . Zudem bestimmt das Vorzeichen vor dem
. Zudem bestimmt das Vorzeichen vor dem 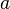 , ob das Wachstum nach oben oder nach unten begrenzt ist.
, ob das Wachstum nach oben oder nach unten begrenzt ist.
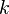 steht für die Wachstumskonstante.
steht für die Wachstumskonstante.
Differenzialgleichung
Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums
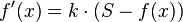 .
.
Erklärung:
Die Differenzialgleichung ausgeschrieben lautet:
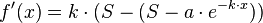
Vereinfacht: