Bewegung in zwei Dimensionen: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(→Vektoren) |
(→Vektor Addition) |
||
| Zeile 46: | Zeile 46: | ||
2. Vektoren die in verschiedene Richtungen wirken: | 2. Vektoren die in verschiedene Richtungen wirken: | ||
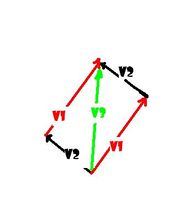
[[Datei:Vektoren1.JPG|rahmenlos|right|Vektoren, die in verschiedene Richtungen wirken]] Vektoren die in verschiedene Richtungen wirken kann man nicht einfach addieren, sondern muss man aufzeichnen und die Enden mit einer Diagonale verbinden. | [[Datei:Vektoren1.JPG|rahmenlos|right|Vektoren, die in verschiedene Richtungen wirken]] Vektoren die in verschiedene Richtungen wirken kann man nicht einfach addieren, sondern muss man aufzeichnen und die Enden mit einer Diagonale verbinden. | ||
| + | |||
| + | <span style="color: red">Die Regel der Vektoraddition genau erklären!</span> | ||
Version vom 18. März 2013, 10:54 Uhr
Inhaltsverzeichnis |
Skalare und Vektoren
Skalare
Skalare sind physikalische Größen, deren Angabe nur durch ihre Größe beschrieben werden. Sie werden durch ihre Menge und Einheit angegeben.
z.B. Energie (E in J/s)
Volumen (V in cm³)
Masse (m in kg)
Leistung. (P in W)
Temperatur (T in °C)
Vektoren
Ein Vektor ist eine physikalische Größe die nicht vollständig durch Angabe ihrer Größe beschrieben wird, sondern zusätzlich zu der Größenangabe noch eine Richtungsangabe hat. Diese Richtungsangabe kennzeichnet man durch einen Pfeil über dem Formelzeichen.
Beispiele:
- Geschwindigkeit
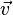in m/s; km/h
- Impuls
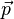in N
- Beschleunigung
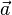in m/s2
Vektor Addition
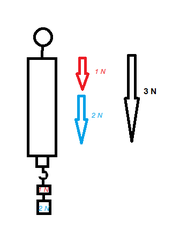
1. Vektoren die entlang einer Linie wirken:
Vektoren die entlang einer Linie wirken und nicht in Verschiedene Richtungen kann man addieren bzw. subtrahieren.
2. Vektoren die in verschiedene Richtungen wirken:
Die Regel der Vektoraddition genau erklären!
