Kurvendiskussion: Unterschied zwischen den Versionen
(→Kriterien für Wendestellen) |
(→Kriterien für Wendestellen) |
||
| Zeile 19: | Zeile 19: | ||
Eine Wendestelle beschreibt einen Punkt im Graphen, an dem sich der Verlauf der Kurve ändert. Die Kurve einer Funktion kann entweder nach links oder nach rechts gekrümmt sein. Diesen Punkt kann man anhand der Ableitungen der Ausgangsfunktion finden. Für eine Wendestelle gibt es zwei Kriterien: | Eine Wendestelle beschreibt einen Punkt im Graphen, an dem sich der Verlauf der Kurve ändert. Die Kurve einer Funktion kann entweder nach links oder nach rechts gekrümmt sein. Diesen Punkt kann man anhand der Ableitungen der Ausgangsfunktion finden. Für eine Wendestelle gibt es zwei Kriterien: | ||
| − | [[ | + | [[File:Inflection point.png|Inflection Point|rahmenlos]] |
* '''Notwendiges Kriterium''' | * '''Notwendiges Kriterium''' | ||
| Zeile 31: | Zeile 31: | ||
| − | ''Fazit für das hinreichende Kriterium | + | ''Fazit für das hinreichende Kriterium'' |
<math>f''' \neq 0</math>, wenn <math>f'''<0</math> dann Rechtskurve, wenn <math>f'''>0</math> dann Linkskurve | <math>f''' \neq 0</math>, wenn <math>f'''<0</math> dann Rechtskurve, wenn <math>f'''>0</math> dann Linkskurve | ||
| + | |||
| + | |||
| + | * '''Beispiel''' | ||
| + | |||
| + | <math>f(x)={1\over9}x^3-{1\over3}x^2-{8\over3}x+{26\over9}</math> | ||
| + | |||
| + | <math>f'(x)={3\over9}x^2-{2\over3}x-{8\over3}</math> | ||
| + | |||
| + | <math>f''(x)={2\over3}x-{2\over3}</math> | ||
| + | |||
| + | <math>f''(x)=0</math> | ||
| + | |||
| + | |||
| + | <math>{2\over3}x-{2\over3}=0</math> <math>\quad</math> <math>|+{2\over3}</math> | ||
| + | |||
| + | <math>{2\over3}x={2\over3}</math> <math>\quad</math> <math>|\cdot{3\over2}</math> | ||
| + | |||
| + | <math>x=1</math> | ||
| + | |||
| + | <math>f(1)={1\over9}\cdot1^3-{1\over3}\cdot1^2-{8\over3}\cdot1+{26\over9}=0</math> | ||
| + | |||
| + | W(1|0) | ||
== vollständige Kurvendiskussion == | == vollständige Kurvendiskussion == | ||
Version vom 11. Dezember 2015, 10:24 Uhr
Inhaltsverzeichnis |
Kriterien für Extremstellen
Definition
Ein Hochpunkt hat den größten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von positiv (+) nach negativ (-) .
Ein Tiefpunkt hat den kleinsten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von negativ (-) nach positiv (+) .
Kriterien
- notwendige Bedingung:
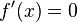
Begründung: Die Ableitung(Steigung) am Extrempunkt ist 0 - hinreichende Bedingung:
- schwache Bedingung:
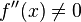
Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. - starke Bedingung: Vorzeichenwechsel an f '(x) an der Stelle des eventuellen Extrempunktes.
Begründung: Die erste Ableitung muss ein Vorzeichenwechsel haben, da sonst ein Sattelpunkt vorliegt.
- schwache Bedingung:
!in Bearbeitung!
Kriterien für Wendestellen
Was ist eine Wendestelle?
Eine Wendestelle beschreibt einen Punkt im Graphen, an dem sich der Verlauf der Kurve ändert. Die Kurve einer Funktion kann entweder nach links oder nach rechts gekrümmt sein. Diesen Punkt kann man anhand der Ableitungen der Ausgangsfunktion finden. Für eine Wendestelle gibt es zwei Kriterien:
- Notwendiges Kriterium
Das notwendige Kriterium wird überprüft, um Stellen herauszufinden, an denen eine Wendestelle vorkommen kann. Dazu bildet man die zweite Ableitung und setzt diese mit Null gleich. Gibt es keine Nullstellen der zweiten Ableitung, so sind alle Wendestellen für die Ausgangsfunktion ausgeschlossen. An Extrema der zweiten Ableitung (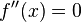
) können aber müssen nicht Wendestellen vorkommen. Um für Gewissheit zu sorgen muss man letztendlich die gefundenen Nullstellen mit dem hinreichenden Kriterium überprüfen.
- Hinreichendes Kriterium
Das hinreichende Kriterium dient zur Bestätigung einer Wendestelle und beschreibt gleichzeitig deren Verlauf (Links-Rechts-Kurve oder Rechts-Links-Kurve). Dazu bildet man die dritte Ableitung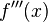 
der Ausgangsfunktion 
und setzt diese gleich mit Null. Ist die dritte Ableitung der zu prüfenden Stelle ungleich 0, so entspricht diese einer Wendestelle. Das Ergebnis dieser Rechnung kann jedoch noch mehr aussagen: Liegt der Wert unter 0, so ist diese eine Links-Rechts-Wendestelle. Liegt der Wert über 0, so entspricht diese einer Rechts-Links-Wendestelle. Falls der Wert jedoch gleich 0 sein sollte, handelt es sich hierbei um keine Wendestelle, sondern um einen sogenannten Sattel- bzw. Terassenpunkt.
Fazit für das hinreichende Kriterium
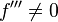, wenn 
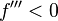dann Rechtskurve, wenn 
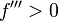dann Linkskurve
- Beispiel
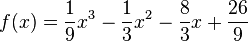
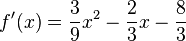
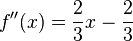
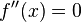
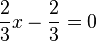
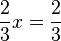
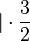
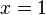
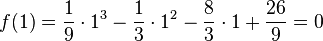
W(1|0)
vollständige Kurvendiskussion
Definitionsbereich
Mit dem Definitionsbereich, sind alle x-Werte gemeint, meist sind es die reellen Zahlen.
Für den Wertebereich gilt das Gleiche, da y von x abhängig ist.
Symmetrie
- Achsensymmetrie zur y-Achse:
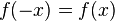
- Punktsymmetrie zum Ursprung:
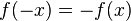
Verschiebung
- um c in x-Richtung
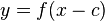
- um d in y-Richtung
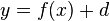
Streckung
- mit Faktor
in x-Richtung: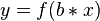 
- mit Faktor a in y-Richtung:
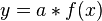
Schnittstellen mit den Achsen
Man setzt die Funktion mit Null gleich und löst die Gleichung nach x auf. Daraus erhält man die Schnittstellen mit der x-Achse (Nullstellen).
Um die Schnittpunkte mit der y-Achse auszurechnen, setzt man für x in der Funktion Null ein und rechnet die Gleichung aus.
Monotonie
=> f streng monoton wachsend
=> f streng monoton fallend
=> f monoton wachsend
=> f monoton fallend
Globalverlauf
- Globalverlauf für gerade Exponenten:
=>
Gesprochen: Für x gegen unendlich, läuft y gegen unendlich
=>
- Globalverlauf für ungerade Exponenten:
Gesprochen: Für x gegen minus unendlich, läuft y gegen minus unendlich
! Anmerkung: Eine negative Basis, bzw. ein negativer Exponent, spiegelt die Kurven an der x-Achse, wodurch auch die Globalverläufe "gespiegelt" werden.
