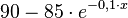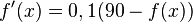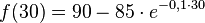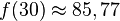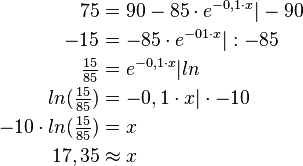Beschränktes Wachstum: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.<br />
 
Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.<br />
 +
 
==Funktionsgleichung==
 
==Funktionsgleichung==
 +
 
===Funktionsterm===
 
===Funktionsterm===
 
<math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br />
 
<math>{f(x)=S-a \cdot e^{-k \cdot x}}</math><br /><br />
Zeile 8: Zeile 10:
 
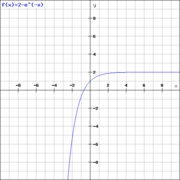
[[Datei:BeWachstum1.png|rahmenlos|links]]
 
[[Datei:BeWachstum1.png|rahmenlos|links]]
 
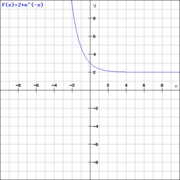
[[Datei:Be Wachstum2.png|rahmenlos|ohne]]<br />
 
[[Datei:Be Wachstum2.png|rahmenlos|ohne]]<br />
 +
 
===Differenzialgleichung===
 
===Differenzialgleichung===
 
Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums<br />
 
Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums<br />
Zeile 20: Zeile 23:
 
Der markierte Teil ist identisch mit <math>{f(x)}</math> und kann daher ersetzt werden:<br />
 
Der markierte Teil ist identisch mit <math>{f(x)}</math> und kann daher ersetzt werden:<br />
 
<math>{f'(x)=k(S-{\color{red}f(x)})}</math><br />
 
<math>{f'(x)=k(S-{\color{red}f(x)})}</math><br />
 +
 
==Beispiel==
 
==Beispiel==
 
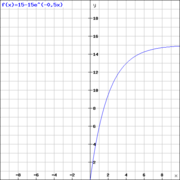
[[Datei:BeWachstum3.png|rahmenlos|rechts]]
 
[[Datei:BeWachstum3.png|rahmenlos|rechts]]
Zeile 26: Zeile 30:
 
(x in Jahren) beschrieben werden.
 
(x in Jahren) beschrieben werden.
 
<br /><br /><br />
 
<br /><br /><br />
 +
 
==Aufgaben==
 
==Aufgaben==
−
{{Aufgabe|Bei Beobachtungsbeginn bedeckt eine Algenart 5 Quadratkilometer des Grundes eines Sees. Die Algen breiten sich innerhalb des 90 Quadratmeter großen Sees aus. Die von den Algen bedeckte Fläche kann mit der Funktion<br />
+
{{Aufgabe|Bei Beobachtungsbeginn bedeckt eine Algenart 5 Quadratkilometer des Grundes eines Sees. Die Algen breiten sich innerhalb des 90 Quadratmeter großen Sees aus. Die von den Algen bedeckte Fläche kann mit der Funktion<br /><br />
−
<math>{90-85 \cdot e^{-0,1 \cdot x}}</math><br />
+
<math>{90-85 \cdot e^{-0,1 \cdot x}}</math><br /><br />
 
(x in Monaten) beschrieben werden.
 
(x in Monaten) beschrieben werden.
 
1) Geben Sie den Funktionsterm als Differenzialsgleichung an!
 
1) Geben Sie den Funktionsterm als Differenzialsgleichung an!
Zeile 42: Zeile 47:
 
3) Wann bedecken die Algen eine Fläche von 75 Quadratkilometern?
 
3) Wann bedecken die Algen eine Fläche von 75 Quadratkilometern?
 
<popup name="Lösung">
 
<popup name="Lösung">
−
<math>{75=90-85 \cdot e^{-0,1 \cdot x}|-90}</math><br />
+
<math> \begin{align}
−
<math>{-15=-85 \cdot e^{-01 \cdot x}|:-85}</math><br />
+
75 &=90-85 \cdot e^{-0,1 \cdot x}|-90 \\
−
<math>{\tfrac{15}{85}=e^{-0,1 \cdot x}|ln}</math><br />
+
-15 &=-85 \cdot e^{-01 \cdot x}|:-85 \\
−
<math>{ln(\tfrac{15}{85}=-0,1 \cdot x| \cdot -10}</math><br />
+
\tfrac{15}{85} &=e^{-0,1 \cdot x}|ln \\
−
<math>{-10 \cdot ln(\tfrac{15}{85}=x}</math><br />
+
ln(\tfrac{15}{85}) &=-0,1 \cdot x| \cdot -10 \\
−
<math>{17,35 \approx x}</math><br />
+
-10 \cdot ln(\tfrac{15}{85}) &=x \\
 +
17,35 & \approx x  
 +
\end{align} </math><br />
 
Nach ungefähr 17,35 Monaten bedecken die Algen 75 Quadratkilometer des Seegrundes.
 
Nach ungefähr 17,35 Monaten bedecken die Algen 75 Quadratkilometer des Seegrundes.
 
</popup>
 
</popup>
 
}}
 
}}

Version vom 5. September 2018, 18:42 Uhr

Beim beschränkten Wachstum nähert sich der Graph einer Schranke an, ohne diese zu berühren oder zu schneiden. Dabei kann sich der Graph sowohl von unten (positives Wachstum) als auch von oben (negatives Wachstum) an die Schranke annähren.

Inhaltsverzeichnis

Funktionsgleichung

Funktionsterm

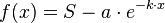
{f(x)=S-a \cdot e^{-k \cdot x}}

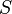{S} steht für die Schranke die nicht überschritten werden kann.
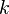{k} steht für die Wachstumskonstante.
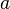{a} steht für den Anfangsbestand, also den Bestand zum Zeitpunkt 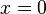{x=0} . Zudem bestimmt das Vorzeichen vor dem 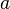{a}, ob das Wachstum nach oben oder nach unten begrenzt ist.

BeWachstum1.png
Be Wachstum2.png

Differenzialgleichung

Als Differenzialgleichung geschrieben lautet der Funktionsterm des beschränkten Wachstums
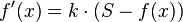{f'(x)=k \cdot (S-f(x))}.

Erklärung:
Die Ableitund des Funktionsterms lautet:
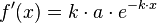
{f'(x)=k \cdot a \cdot e^{-k \cdot x}}
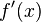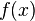Um daraus eine Differenzialgleichung zu machen, muss neben {f'(x)} auch {f(x)} in der Funktion enthalten sein. Dafür muss diese zuerst umgeformt werden:
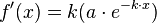
{f'(x)=k(a \cdot e^{-k \cdot x})}
Jetzt fehlt nur noch die Schranke 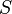{S}:
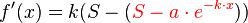
{f'(x)=k(S-({\color{red}S-a \cdot e^{-k \cdot x}}))}
Der markierte Teil ist identisch mit 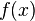{f(x)} und kann daher ersetzt werden:
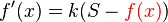
{f'(x)=k(S-{\color{red}f(x)})}

Beispiel

BeWachstum3.png

Nach dem Einpflanzen wächst ein Baum recht schnell, jedoch wächst er langsamer je größer er wird, sodass sich seine Höhe einer natürlichen Grenze annähert. Diese Höhe (in Metern) kann mit der Funktion
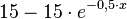
{15-15 \cdot e^{-0,5 \cdot x}}
(x in Jahren) beschrieben werden.


Aufgaben

30px   Aufgabe

Bei Beobachtungsbeginn bedeckt eine Algenart 5 Quadratkilometer des Grundes eines Sees. Die Algen breiten sich innerhalb des 90 Quadratmeter großen Sees aus. Die von den Algen bedeckte Fläche kann mit der Funktion

{90-85 \cdot e^{-0,1 \cdot x}}

(x in Monaten) beschrieben werden. 1) Geben Sie den Funktionsterm als Differenzialsgleichung an!

2) Welche Fläche bedecken die Algen nach zweieinhalb Jahren?

3) Wann bedecken die Algen eine Fläche von 75 Quadratkilometern?

Von „http://fsg.zum.de/index.php?title=Beschränktes_Wachstum&oldid=1804“