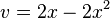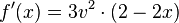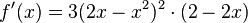Ableitungsregeln: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Kettenregel)
(→‎Kettenregel)
Zeile 28: Zeile 28:
 
<br />
 
<br />
 
<math>f(x)=u(v(x))</math><br />
 
<math>f(x)=u(v(x))</math><br />
−
<math>f'(x)=u'\cdotv\cdotv'</math>
 
 
<br />
 
<br />
−
Beispiel 1:<br />
+
<math>f'(x)=u'(v) \cdot v'(x)</math><br />
 +
<br />
 +
Die Ableitung einer verketteten Funktion ist die Ableitung <br />
 +
der äußeren Funktion mal der Ableitung der inneren Funktion.
 +
<br />
 +
<br />
 +
Beispiel:<br />
 
<math>f(x)=(2x-x^2)^3</math><br />
 
<math>f(x)=(2x-x^2)^3</math><br />
 
<br />
 
<br />

Version vom 6. März 2012, 09:00 Uhr


Bekannte Ableitungsregeln aus Klasse 10

Potenzregel

Summenregel

Datei:Http://upload.wikimedia.org/wikipedia/de/math/e/b/8/eb8e7da7c480129c2d56f9a4502a515e.png

Faktorregel

Neue Ableitungsregeln

Produktregel

Allgemeine Formel der Produktregel
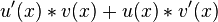
u'(x)*v(x)+u(x)*v'(x)

Quotientenregel

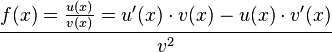
f(x)= {u(x) \over v(x)}= u'(x)\cdot v(x)-{u(x)\cdot v'(x)} \over v^2 

Im Nenner steht die Ableitung von u(x) welche mit v(x) multiplizert wird und von u(x) welches mit der Ableitung von v(x) multipliziert wird, subtrahiert.

Kettenregel

Allgemeine Formel der Kettenregel:

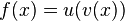
f(x)=u(v(x))

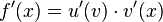
f'(x)=u'(v) \cdot v'(x)

Die Ableitung einer verketteten Funktion ist die Ableitung
der äußeren Funktion mal der Ableitung der inneren Funktion.

Beispiel:
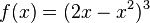
f(x)=(2x-x^2)^3

äußere Funktion: 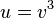u=v^3
innere Funktion: v=2x-2x^2

f'(x)=3v^2\cdot(2-2x)

f'(x)=3(2x-x^2)^2\cdot(2-2x)

Von „http://fsg.zum.de/index.php?title=Ableitungsregeln&oldid=540“