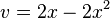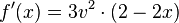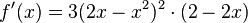Ableitungsregeln: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(→Kettenregel) |
(→Quotientenregel) |
||
| Zeile 19: | Zeile 19: | ||
<math> | <math> | ||
| − | f(x)= {u(x) \over v(x)}= u'(x)\cdot v(x)- | + | f(x)= {u(x)\over v(x)}= {{u'(x) \cdot v(x)- u(x) \cdot v'(x)} \over {v^2}} |
</math> | </math> | ||
| − | + | <math> Kurzform: f'(x)= {{u' \cdot v- u \cdot v' } \over {v^2}} </math> | |
=== Kettenregel === | === Kettenregel === | ||
Version vom 6. März 2012, 09:02 Uhr
Bekannte Ableitungsregeln aus Klasse 10
Potenzregel
Summenregel
Datei:Http://upload.wikimedia.org/wikipedia/de/math/e/b/8/eb8e7da7c480129c2d56f9a4502a515e.png
Faktorregel
Neue Ableitungsregeln
Produktregel
Allgemeine Formel der Produktregel
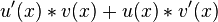
Quotientenregel
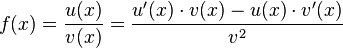
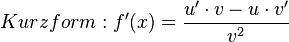
Kettenregel
Allgemeine Formel der Kettenregel:
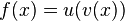
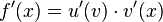
Die Ableitung einer verketteten Funktion ist die Ableitung
der äußeren Funktion mal der Ableitung der inneren Funktion.
Beispiel:
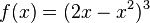
äußere Funktion: 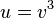
innere Funktion: