Tangentenprobleme: Unterschied zwischen den Versionen
(→Tangente - Definition und Tangentengleichung) |
(→Tangente - Definition und Tangentengleichung) |
||
| Zeile 12: | Zeile 12: | ||
<math>y=f'(x_0)*(x-x_0)+f(x_0)</math><br /> | <math>y=f'(x_0)*(x-x_0)+f(x_0)</math><br /> | ||
<br /> | <br /> | ||
| − | P(x|y) ist der Punkt der Tangente. | + | P(x|y) ist der Punkt der Tangente.<br /><br /> |
| + | Beispiel:<br /> | ||
| + | Gegeben ist eine Funktion F und ein Punkt P, der nicht zu f gehört.<br /> | ||
| + | Finde die Tangente von P an f, ohne den Berührpunkt zu kennen.<br /> | ||
| + | <math>f(x)=\frac{-x^2}{4}(x-6)</math> P(6|0)<br /> | ||
| + | allgemeine Tangentengleichung:<br /> | ||
| + | <math>y=f'(x_0)*(x-x_0)+f(x_0)</math><br /> | ||
| + | <math>P(x|y) P(6|0)</math> ---> Punkte der Tangente<br /> | ||
| + | <math>P_0(x_0|y_0)</math>= unbekannter Berühpunkt der Tangente<br /> | ||
| + | <math>0=\frac{-2x}{4}(x-6)-\frac{x_0^2}{4}*1*(6-x_0)+(-\frac{x_0^2}{4} (x_0-6))</math><br /> | ||
| + | Gleichung in GTR eingeben:<br /> | ||
| + | Berührpunkte:<br /> | ||
| + | <math>x_1=0</math><br /> | ||
| + | <math>x_2=0</math><br /> | ||
| + | Einsetzt x_2 in die allgemeine Tangentengleichung:<br /> | ||
| + | ---> <math>y=(-\frac{2*0}{4}(0-6)-\frac{0^2}{4}*1*(x-0)+0)</math><br /> | ||
| + | Tangentengleichung: <math>y=0*x+0</math><br /> | ||
| + | Das Ergebnis für x=6: y=0 | ||
== Tangente an Schaubild, Berührpunkt ist bekannt == | == Tangente an Schaubild, Berührpunkt ist bekannt == | ||
Version vom 19. Juni 2012, 07:46 Uhr
Tangente - Definition und Tangentengleichung
Definition
Gegeben ist ein Punkt 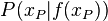 auf dem Schaubild einer differenzierbaren Funktion f. Die Tangente des Schaubildes im Punkt P ist genau diejenige Gerade durch P mit
auf dem Schaubild einer differenzierbaren Funktion f. Die Tangente des Schaubildes im Punkt P ist genau diejenige Gerade durch P mit 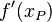 als Steigung.
als Steigung.
Allgemeine Tangentengleichungen:
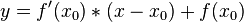
P(x|y) ist der Punkt der Tangente.
Beispiel:
Gegeben ist eine Funktion F und ein Punkt P, der nicht zu f gehört.
Finde die Tangente von P an f, ohne den Berührpunkt zu kennen.
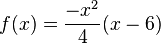 P(6|0)
P(6|0)
allgemeine Tangentengleichung:
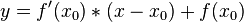
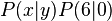 ---> Punkte der Tangente
---> Punkte der Tangente
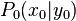 = unbekannter Berühpunkt der Tangente
= unbekannter Berühpunkt der Tangente
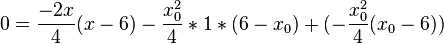
Gleichung in GTR eingeben:
Berührpunkte:
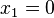
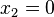
Einsetzt x_2 in die allgemeine Tangentengleichung:
---> 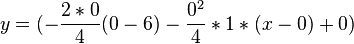
Tangentengleichung: 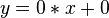
Das Ergebnis für x=6: y=0
Tangente an Schaubild, Berührpunkt ist bekannt
30px Aufgabe
Bestimme die Gleichung der Tangente, die am Schaubild der Funktion |
Tangente an Schaubild, Steigung ist bekannt
30px Aufgabe
Gegeben ist die Funktion f mit |
Tangente an Schaubild, Berührpunkt unbekannt
30px Aufgabe
Vom Punkt |
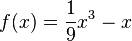 an der Stelle
an der Stelle 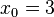 angelegt werden kann.
angelegt werden kann.
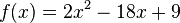 . Gib die Gleichungen aller Tangenten mit der Steigung
. Gib die Gleichungen aller Tangenten mit der Steigung 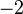 an, die an das Schaubild von f gelegt werden können.
an, die an das Schaubild von f gelegt werden können.
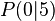 aus werden Tangenten an das Schaubild von
aus werden Tangenten an das Schaubild von 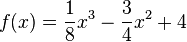 gelegt. Bestimme die Gleichungen dieser Tangenten und die Koordinaten der Berührpunkte.
gelegt. Bestimme die Gleichungen dieser Tangenten und die Koordinaten der Berührpunkte.

