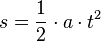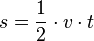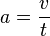Geradlinige Bewegung: Unterschied zwischen den Versionen

Version vom 4. Dezember 2012, 12:39 Uhr

Man kann diese Bewegung in zwei Kategorien einteilen:

• Bewegung mit konstanter Geschwindigkeit

• Beschleunigte Bewegungen darunter fällt:

    *gleichmäßig Beschleunigung 
    *

geradlinig gleichförmige Bewegung

Geradlinige gleichförmige Bewegungen gibt es, wenn sich ein Körper mit einer konstanter Geschwindigkeit fort bewegt, deshalb gibt es im s/t Diagramm eine eine Gerade, welche man mit einer liniaren Funktion beschreien kann.

Diagramme einer gleichförmigen Bewegung

in Bearbeitung

Formeln einer gleichförmigen Bewegung

Ein Fahrzeug mit gleichbleibender Geschwindigkeit bewegt sich pro Zeiteinheit immer um die selbe Strecke fort. Deshalb gilt die allgemeine Formel:

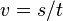
Durch einfaches mathematisches Umstellen kann man sich so auch die Formeln für die Strecke und die Zeit bei konstanter Geschwindigkeit herleiten.

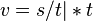
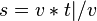
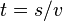
Anwendungsbeispiele gleichförmiger Bewegungen

Ein Fahrrad bewegt sich mit konstanter Geschwindigkeit um eine Strecke von 16m. Alle zwei Meter wird eine Zeitmessung unternommen und die Werte aufgeschrieben.

Strecke: s in m 0 2 4 6 8 10 12 14 16 Lauf 1: t in s 0 0,38 0.98 1,29 1,78 2,3 2,61 3,18 3,98

Lauf 2: t in s 0 0,74 1,56 2,22 3,06 3,99 4,46 5,0 6,64

Bestimme die Steigung der Graphen und damit die Geschwindigkeit.

geradlinig gleichmäßig beschleunigte Bewegung

Diagramme einer gleichmäßig beschleunigten Bewegung

in Bearbeitung (Geh weg Effe)

Formeln einer gleichmäßig beschleunigten Bewegung

Anwendungsbeispiele beschleunigter Bewegungen

Freier Fall