Bernoulli Experiment und Bernoulli Kette
Bernoulli Experiment:
Ein Bernoulli Experiment ist ein Zufallsexperiment, bei dem es immer zwei mögliche Versuchsausgänge gibt. Die Wahrscheinlichkeiten für beide Ausgänge ergeben addiert Eins.
Beispiel 1:
Man wirft eine nicht manipulierte Münze.
Es gibt zwei mögliche Versuchsausgänge: Kopf oder Zahl. Die Wahrscheinlichkeit für Kopf und Zahl ist jeweils  . Addiert man die beiden Wahrscheinlichkeiten, so erhält man Eins.
. Addiert man die beiden Wahrscheinlichkeiten, so erhält man Eins.
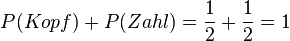
Beispiel 2:
Man wirft eine manipulierte Münze.
Es gibt wieder zwei mögliche Versuchsausgänge: Kopf oder Zahl. Die Wahrscheinlichkeit für Kopf beträgt nun jedoch  . Die Wahrscheinlichkeit für Zahl beträgt hingegen
. Die Wahrscheinlichkeit für Zahl beträgt hingegen  . Addiert man die beiden Wahrscheinlichkeiten, so erhält man ebenfalls Eins.
. Addiert man die beiden Wahrscheinlichkeiten, so erhält man ebenfalls Eins.
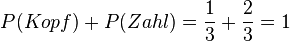
Bernoulli Kette:
Als Bernoulli Kette bezeichnet man die Wiederholung eines Bernoulli Experimentes unter gleich bleibenden Voraussetzungen. Diese Wiederholung kann beliebig oft sein.
Beispiel:
Man wirft eine Münze zehnmal hintereinander. Es handelt sich nun um eine Bernoulli Kette mit zehn Wiederholungen.
Quelle: http://www.frustfrei-lernen.de/mathematik/bernoulli-experiment-kette.html

