Kurvendiskussion
Inhaltsverzeichnis |
Kriterien für Extremstellen
Definition
Ein Hochpunkt hat den größten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von positiv (+) nach negativ (-) .
Ein Tiefpunkt hat den kleinsten y-Wert in seiner Umgebung. Außerdem hat die erste Ableitung einen Vorzeichenwechsel von negativ (-) nach positiv (+) .
Kriterien
- notwendige Bedingung:
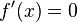
Begründung: Die Ableitung(Steigung) am Extrempunkt ist 0 - hinreichende Bedingung:
- schwache Bedingung:
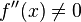
Begründung: Die zweite Ableitung darf nicht 0 sein, da sonst kein Extrempunkt, sondern ein Sattelpunkt vorliegt. - starke Bedingung: Vorzeichenwechsel an f '(x) an der Stelle des eventuellen Extrempunktes.
Begründung: Die erste Ableitung muss ein Vorzeichenwechsel haben, da sonst ein Sattelpunkt vorliegt.
- schwache Bedingung:
!in Bearbeitung!
Kriterien für Wendestellen
vollständige Kurvendiskussion
Definitionsbereich
Mit dem Definitionsbereich, sind alle x-Werte gemeint, meist sind es die reellen Zahlen.
Für den Wertebereich gilt das Gleiche, da y von x abhängig ist.
Symmetrie
- Achsensymmetrie zur y-Achse:
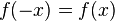
- Punktsymmetrie zum Ursprung:
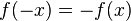
Verschiebung
- um c in x-Richtung
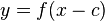
- um d in y-Richtung
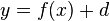
Streckung
- mit Faktor
 in x-Richtung:
in x-Richtung: 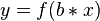
- mit Faktor a in y-Richtung:
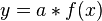
Schnittstellen mit den Achsen
Man setzt die Funktion mit Null gleich und löst die Gleichung nach x auf. Daraus erhält man die Schnittstellen mit der x-Achse (Nullstellen).
Um die Schnittpunkte mit der y-Achse auszurechnen, setzt man für x in der Funktion Null ein und rechnet die Gleichung aus.
Monotonie
=> f streng monoton wachsend
=> f streng monoton fallend
=> f monoton wachsend
=> f monoton fallend
Globalverlauf
- Globalverlauf für gerade Exponenten:
=>
Gesprochen: Für x gegen unendlich, läuft y gegen unendlich
=>
Gesprochen: Für x gegen minus unendlich, läuft y gegen unendlich
- Globalverlauf für ungerade Exponenten:
=>
Gesprochen: Für x gegen unendlich, läuft y gegen unendlich
=>
Gesprochen: Für x gegen minus unendlich, läuft y gegen minus unendlich
! Anmerkung: Eine negative Basis, bzw. ein negativer Exponent, spiegelt die Kurven an der x-Achse, wodurch auch die Globalverläufe "gespiegelt" werden.

