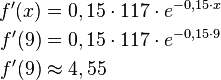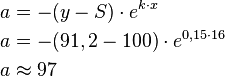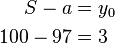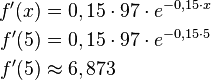Beschränktes Wachstum
Beim beschränkten Wachstum ist die Änderungsrate proportional zum Sättigungsmanko.
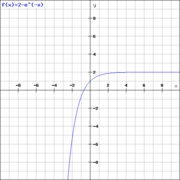
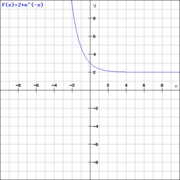
Der Graph der Funktion eines beschränkten Wachstums nähert sich einer Schranke an. Der Abstand zwischen Graph und Schranke wird Sättigungsmanko genannt.
Ist das Wachstum nach oben beschränkt, so nähert sich der Graph von unten an die Schranke an. Die Steigung des Graphen ist dabei positiv und wird umso geringer, je weiter sich der Graph der Schranke annähert.
Ist das Wachstum nach unten beschränkt, so nähert sich der Graph von oben an die Schranke an. Die Steigung des Graphen ist dabei negativ und wird umso größer, je weiter sich der Graph der Schranke annähert.
Inhaltsverzeichnis[Verbergen] |
Funktionsterm
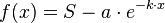
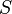 steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.
steht für die Schranke, der sich der Graph annähert, die aber nicht überschritten werden kann.
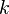 steht für die Wachstumskonstante.
steht für die Wachstumskonstante.
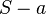 ergeben den Anfangsbestand, also den Bestand zum Zeitpunkt
ergeben den Anfangsbestand, also den Bestand zum Zeitpunkt 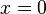 . Zudem bestimmt das Vorzeichen vor dem
. Zudem bestimmt das Vorzeichen vor dem 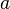 , ob das Wachstum nach oben oder nach unten begrenzt ist.
, ob das Wachstum nach oben oder nach unten begrenzt ist.
a berechnen
Um den Anfangsbestand zu berechnen, muss der restliche Funktionsterm auf 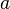 umgeformt werden.
umgeformt werden.
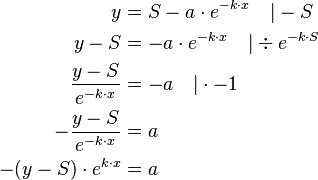
Beispiel
Gegeben ist die Gleichung
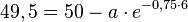
Um den Anfangsbestand zu berechnen müssen die Werte in die umgeformte Gleichung eingesetzt werden.
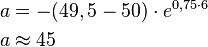
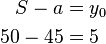
Der Anfangsbestand ist also 5.
30px Aufgabe
Gegeben ist die Gleichung |
Wachstumsgeschwindigkeit berechnen
Um die Wachstumsgeschwindigkeit zu berechnen, muss die Ableitung gebildet werden.
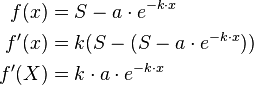
Beispiel
Gegeben ist die Funktionsgleichung
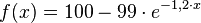
Also lautet die Ableitungsfunktion
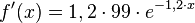
Damit lässt sich die Wachststumsgeschwindigkeit der Ausgangsgleichung an jeder beliebigen Stelle berechnen.
30px Aufgabe
Gegeben ist die Funktionsgleichung |
Übungsaufgabe
Auf dem Grund eines Sees mit einer Fläche von 100 km² breitet sich eine neue Algenart aus. Sie ist auf die Fläche des Sees begrenzt. Ihr Wachstum kann mit der Funktion
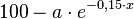
beschrieben werden.
a)Berechnen Sie den Anfangsbestand, wenn die Algenart nach 16 Jahren 91,2 km² des Sees bedeckt!
b)Wie hoch ist die Wachstumsgeschwindigkeit am Ende des 5. Jahres?
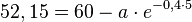
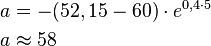
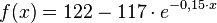
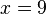 an!
an!