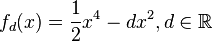Funktionenscharen
Die folgenden Kapitel werden anhand einer Aufgabe erklärt.
30px Aufgabe
Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte? |
Funktionenscharen
Berechnung der Extrempunkte:
f(x)= {1 \over 2x^4-dx^2
f'(x)= 2x^3-2dx
f(x)= 6x^2-2d
2x^3-2dx= 0
2x^3= 2dx
x^3 = dx
x^2= d
x= 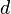 -> d kann nicht negativ sein
f(x) > 0 TP f(x) < 0 HP
-> d kann nicht negativ sein
f(x) > 0 TP f(x) < 0 HP
f(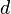 )= 6(
)= 6(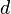 )^2-2d
= 6d-2d
=4d
d < 0 -> HP
d > 0 -> TP
)^2-2d
= 6d-2d
=4d
d < 0 -> HP
d > 0 -> TP
Ortskurven
Bestimmung der Ortskurve der Hochpunkte:
Ortskurven sind Kurven, auf denen Punkte mit gleichen Eigenschaften einer Kurvenschar liegen z.B alle Hochpunkte.
Bestimmen von Ortskurven
Die Koordinaten des Extrempunktes sind E1 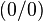 E2
E2 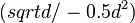 E3
E3 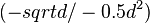
Koordinaten der Extrempunkte einzeln aufschreiben:
x = 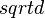
f 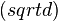 =
= 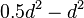
x - Koordinate nach Parameter auflösen:
d = 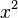
Diesen Parameter in die y - Gleichung einsetzen:
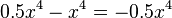
Gleichung der Ortskurve der Extrempunkte:
y =