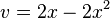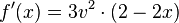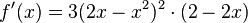Ableitungsregeln

Bekannte Ableitungsregeln aus Klasse 10

Potenzregel

Allgemeine Formel:

$f(x)=x^n$
$f'(x)=n \cdot x^{n-1}$

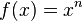
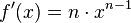
Beispiel:

$f(x)=x^3+x^2-x$
$f'(x)=3x^2+2x-1$

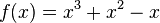
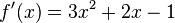
Summenregel

Allgemeine Formel:

$\begin{align} f(x)&=u(x)+v(x) \\ f'(x)&=u'(x) + v'(x) \end{align}$

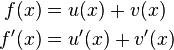
Faktorregel

Allgemeine Formel:

$f(x)=ax^n$
$f'(x)=a \cdot n \cdot x^{n-1}$

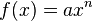
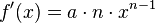
Bespiel:

$f(x)=2x^3+4x^2+5x$
$f'(x)=6x^2+8x+5$

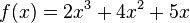
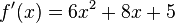
Neue Ableitungsregeln

Produktregel

Vorsicht: Was ist die Ausgangsfunktion? [Btm]

Allgemeine Formel:

$f(x)=u(x) \cdot v(x)$

$f'(x)=u'(x)\cdot v(x)+u(x)\cdot v'(x)$

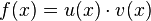
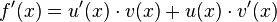
Kurzform: 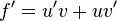$f'=u'v+uv'$


Rechenbeispiel:
$f(x)=(5x^2) \cdot x^{1 \over 2}$
$f'(x)=(10x) \cdot (x^{1 \over 2})+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}$
$f'(x)=10x \cdot sqrt{x}+(5x^2) \cdot {1 \over 2}x^{-{1 \over 2}}$

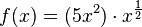
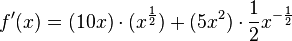
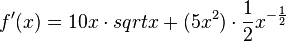
Kann man das noch weiter umschreiben? [Btm]

Quotientenregel

Vorsicht: typischer Formulierungsfehler! [Btm]

$f(x)= {u(x)\over v(x)}$
$f'(x)= {{u'(x) \cdot v(x)- u(x) \cdot v'(x)} \over (v(x))^2}$

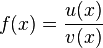
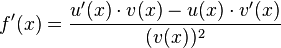
Kurzform:
$f'= {{u' \cdot v- u \cdot v' } \over {v^2}}$

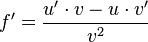
Kettenregel

Allgemeine Formel der Kettenregel:

$f(x)=u(v(x))$

$f'(x)=u'(v) \cdot v'(x)$

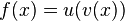
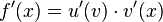
Die Ableitung einer verketteten Funktion ist die Ableitung
der äußeren Funktion mal der Ableitung der inneren Funktion.

Beispiel:

$f(x)=(2x-x^2)^3$

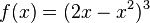
äußere Funktion: 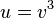$u=v^3$
innere Funktion: $v=2x-2x^2$

$f'(x)=3v^2\cdot(2-2x)$

$f'(x)=3(2x-x^2)^2\cdot(2-2x)$