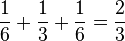Ereignisbaum

Ereignisbäume werden angefertigt um die Wahrscheinlichkeit eines Experimentes zu veranschaulichen. Um die Wahrscheinlichkeit für ein Ereignis zu erfahren muss man die Wahrscheinlichkeiten auf dem Pfad vom Anfang bis zum gesuchten Ereignis addieren. Ein Ereignisbaum kann wie in den folgenden Beispielen aussehen.
Beispiel 1:
In einem Gefäß befinden sich 3 Kugeln, einer roten, einer schwarzen und einer grünen. Man zieht zwei Mal eine Kugle ohne zu sehen welche Farbe diese hat. Wurde eine Kugel heraus genommen, so wird sie wieder zurück gelegt.

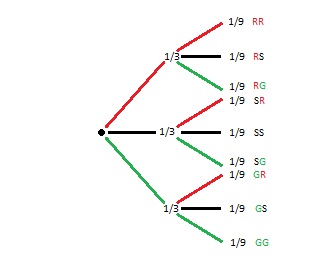
einige Wahrscheinlichkeiten:
Gleichfarbige (RR+SS+GG): 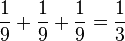$\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{1}{3}$
nur Rote (RR): $\frac{1}{9}$
eine Rote und eine Grüne (RG+GR): 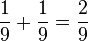$\frac{1}{9}+\frac{1}{9}=\frac{2}{9}$
mindestens ein Schwarz(RS+SR+SS+SG+GS): 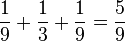$\frac{1}{9}+\frac{1}{3}+\frac{1}{9}=\frac{5}{9}$
Beispiel 2:
In einem Gefäß befinden sich 3 Kugeln, einer roten, einer schwarzen und einer grünen. Man zieht zwei Mal eine Kugle ohne zu sehen welche Farbe diese hat. Wurde eine Kugel heraus genommen, so bleibt sie draußen.

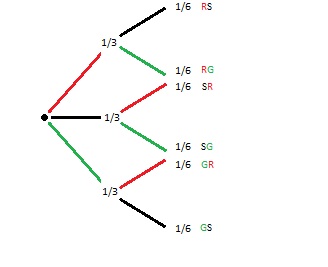
einige Wahrscheinlichkeiten:
eine Rote und eine Grüne(RG+GR): 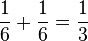$\frac{1}{6}+\frac{1}{6}=\frac{1}{3}$
mind. eine Schwarze(RS+SR+SG+GS): $\frac{1}{6}+\frac{1}{3}+\frac{1}{6}=\frac{2}{3}$