Abstand zwischen zwei Punkten

Abstand zwischen zwei Punkten

Definition

---

Im Vektorraum können Punkte, Geraden und Flächen veranschaulicht werden und ihre Abstände zueinander bestimmt werden. Unter dem Abstand versteht man die Länge der kürzesten Verbindungstrecke zwischen zwei Objekten.

Hat man zwei Punkte im Raum, so lässt sich ihr Abstand mit Hilfe des Satzes von Pythagoras berechnen.



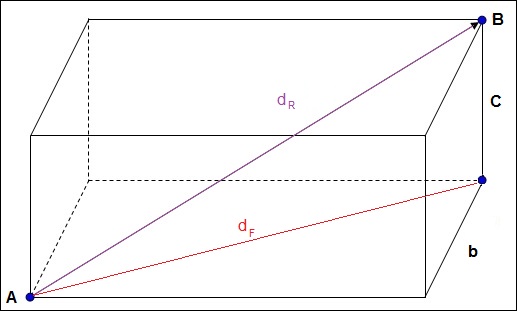
Spannt man einen Quader zwischen die Punkte, so enstpricht der Abstand der Länge der Raumdiagonalen.
Es gilt:
$d_F^2 = a^2+b^2$

$d_R^2 = d_F^2+c^2$

=>$d_R^2 = a^2+b^2+c^2$

$d_R = \sqrt{a^2+b^2+c^2}$

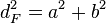
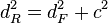
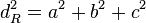
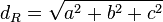
Daher gilt: 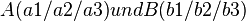$A(a1/a2/a3)und B(b1/b2/b3)$

Um den Abstand zu berechnen muss zuerst der Vetor 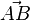$\vec{AB}$ gebildet werden:

$\vec{AB} = \begin{pmatrix} b1-a1 \\ b2-a2 \\ b3-a3 \end{pmatrix}$

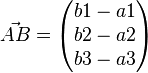
dieser entspricht der Raumdiagonalen.

Die Lage des Vektors ist demnach:

$\vec{\left| AD \right| } = \sqrt {(b1-a1)^2+(b2-a2)^2+(b3-a3)^2}$

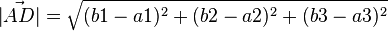
Vorsicht, Fehler! [Btm]

Beispiel:
$A(5/8/3) und B(8/10/9)$

$\vec{AB} = \begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix}$

$\vec{\left| AD \right| } = \sqrt{3^2+2^2+6^2} = \sqrt {49} = 7$

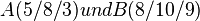
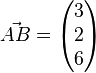
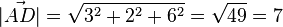
A: Der Abstand beträgt 7 Längeneinheiten.