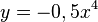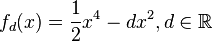Funktionenscharen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Die folgenden Kapitel werden anhand einer Aufgabe erklärt. {{Aufgabe|1=Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher…“) |
(→Beispiel Nr. 1) |
||
| (35 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{Aufgabe|1=Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte?<br/> | {{Aufgabe|1=Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte?<br/> | ||
| − | <math>f_d (x)= {1 \over 2} x^4 -d x^2 </math> | + | <math>f_d (x)= {1 \over 2} x^4 -d x^2, d \in \mathbb{R} </math> |
}} | }} | ||
== Funktionenscharen == | == Funktionenscharen == | ||
| + | '''Berechnung der Extrempunkte:''' <br /> | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | f(x)&=& {1 \over 2} x^4-dx^2 \\ | ||
| − | == | + | f'(x)&=& 2x^3-2dx \\ |
| + | f''(x)&=& 6x^2-2d | ||
| + | \end{matrix} | ||
| + | </math> | ||
| − | <!-- | + | <br /> |
| − | <ggb_applet width="754" height="631" version="4.0" ggbBase64=" | + | |
| + | <math> | ||
| + | \begin{matrix} | ||
| + | 2x^3-2dx&=& 0 & \\ | ||
| + | 2x^3&=& 2dx &\\ | ||
| + | x^3 &=& dx & x_1 = 0\\ | ||
| + | x^2&=& d &\\ | ||
| + | x_2&=& \sqrt d &\\ | ||
| + | x_3&=& - \sqrt d & d \not< 0 | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | |||
| + | <br /> | ||
| + | |||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | f''(x) &>& 0 \rightarrow TP \\ | ||
| + | f''(x) &<& 0 \rightarrow HP | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math>f''( \sqrt d) = 6 (\sqrt d)^2-2d = 6d-2d =4d </math><br /> | ||
| + | <math>f''(-\sqrt d)= 6 (-\sqrt d) ^2-2d=6d-2d=4d</math> <br /> | ||
| + | <math> 4d > 0 \rightarrow TP </math> für beide Extrempunkte <br /> | ||
| + | für <math> d = 0 </math> liegt kein Tiefpunkt vor! | ||
| + | |||
| + | |||
| + | <math>f''( 0) = -2d</math><br /> | ||
| + | <math> -2d < 0 \rightarrow HP </math> , für <math> d = 0 </math> liegt kein Hochpunkt vor! | ||
| + | |||
| + | = Ortskurven = | ||
| + | |||
| + | === Allgemeine Herleitung einer Ortskurve === | ||
| + | |||
| + | ==== Hoch- bzw Tiefpunkt bestimmen ==== | ||
| + | -> Die 1. Ableitung 0 setzen | ||
| + | -> Ergebnis in die 2. Ableitung einsetzen | ||
| + | -> Ergebnis größer 0 -> Tiefpunkt; | ||
| + | Ergebnis kleiner 0 -> Hochpunkt | ||
| + | ==== Ortskurve bestimmen ==== | ||
| + | -> x-Koordinate in die Funktion einsetzen | ||
| + | -> Ergebnis bildet die y-Koordinate | ||
| + | -> x-Koordinate nach t auflösen | ||
| + | -> t Auflösung in y einsetzen | ||
| + | -> Lösung = Ortskurvenfunktion | ||
| + | |||
| + | ==== Probe mit Hilfe des GTRs ==== | ||
| + | -> In "Y=" für y<sub>1,2,3</sub> für t in der Funktion beliebige Zahlen einsetzen (z.B. 1,2 und 3) | ||
| + | -> Ortskurvenfunktion in y<sub>4</sub> einsetzen | ||
| + | -> Im "Graph" überprüfen, ob die Ortskurve alle Funktionen an derselben Stelle durchläuft | ||
| + | |||
| + | ==== Beispiel Nr. 1 ==== | ||
| + | <math>f_t(x)=x^2+tx</math> | ||
| + | <br /> | ||
| + | <math>f'_t(x)=2x+t</math> | ||
| + | <br /> | ||
| + | <math>f''_t(x)=2</math> | ||
| + | <br /><br /> | ||
| + | |||
| + | Hoch- bzw Tiefpunkt bestimmen: | ||
| + | <br /> | ||
| + | <math>f'_t(x)= 2x+t=0</math> | ||
| + | <br /> | ||
| + | <math>2x=t</math> | ||
| + | <br /> | ||
| + | <math>x=-{t \over2}</math> | ||
| + | <br /><br /> | ||
| + | |||
| + | Kurvenverhalten: | ||
| + | <br /> | ||
| + | <math>f''_t(x)=2</math> | ||
| + | <br /> | ||
| + | größer als 0 -> Tiefpunkt | ||
| + | <br /><br /> | ||
| + | |||
| + | Ortskurve bestimmen: | ||
| + | <br /> | ||
| + | <math>f_t \left({t \over2}\right)=\left(-{t \over2}\right)^2+t\cdot\left(-{t \over2}\right)</math> | ||
| + | <br /> | ||
| + | <math>=\left(-{t \over2}\right)\cdot\left({t \over2}\right)+t\cdot\left({t \over2}\right)</math> | ||
| + | <br /> | ||
| + | <math>={t^2 \over4}-{t^2 \over2}</math> | ||
| + | <br /> | ||
| + | <math>-{t^2 \over4}</math> | ||
| + | |||
| + | <math>TP \left(-{t \over2} ; -{t^2 \over4}\right)</math> | ||
| + | <br /><br /> | ||
| + | x-Koordinate nach t auflösen: | ||
| + | <br /> | ||
| + | <math>x=-{t \over2}</math> | ||
| + | <br /> | ||
| + | <math>t=-2x</math> | ||
| + | <br /><br /> | ||
| + | t Auflösung in y einsetzen: | ||
| + | <br /> | ||
| + | <math>y=-{t^2 \over4}</math> | ||
| + | <br /> | ||
| + | <math>y=-{(-2x)^2 \over4}</math> | ||
| + | <br /> | ||
| + | <math>=-{(-2x)\cdot(-2x) \over4}</math> | ||
| + | <br /> | ||
| + | <math>=-{4x^2 \over4}</math> | ||
| + | <br /> | ||
| + | <math>=-x^2</math> --> Ortskurvenfunktion | ||
| + | <br /><br /> | ||
| + | Probe mit Hilfe des GTRs! | ||
| + | <br /> | ||
| + | [[Datei:Ortskurven Beispiel 1.jpg|thumb|locus curve]] | ||
| + | <br /> | ||
| + | [[Benutzer:MeJvzm-fsg|MeJvzm-fsg]] ([[Benutzer Diskussion:MeJvzm-fsg|Diskussion]]) 10:21, 11. Dez. 2015 (CET) M.Entenmann | ||
| + | |||
| + | |||
| + | '''Beispiel Nr. 2''' | ||
| + | |||
| + | '''Bestimmen von Ortskurven''' | ||
| + | |||
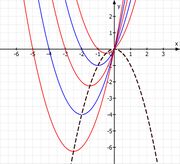
| + | Die Koordinaten des Extrempunktes sind <math> E_1 ( 0 | 0 ) </math>, <math> E_2 ( \sqrt d | - 0,5 d^2) </math>, <math> E_3 ( -\sqrt d | - 0,5 d^2) </math> | ||
| + | |||
| + | |||
| + | Koordinaten der Extrempunkte einzeln aufschreiben: | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | x&=\sqrt d \\ | ||
| + | y&= f( \sqrt d ) = - 0,5 d^2 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | x - Koordinate nach Parameter auflösen: | ||
| + | |||
| + | <math>d= x^2 </math> | ||
| + | |||
| + | |||
| + | Diesen Parameter in die y - Gleichung einsetzen: | ||
| + | |||
| + | <math>y= -0,5x^4 </math> | ||
| + | |||
| + | |||
| + | Gleichung der Ortskurve der Extrempunkte: | ||
| + | |||
| + | <math>y= -0,5 x^4 </math> | ||
| + | |||
| + | |||
| + | <!-- Bitte unbedingt stehen lassen und nicht verändern - das ist die Grafik!!! --> | ||
| + | <ggb_applet width="754" height="631" version="4.0" ggbBase64="UEsDBBQACAAIAJqZZkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACamWZAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1YbY/TRhD+DL9i5A8VVCTZtdd2AgkIkFCRDqh0tKr6odXG3iTL2V7LXuflxI/v7K7tODm4ckBRI3L7Njuz88xrmD/b5xlsRVVLVSw8OiYeiCJRqSzWC6/Rq9HUe/b0/nwt1FosKw4rVeVcLzxmKGW68EKxDMkqJKNotpqOGAnS0ZT4yYiyeEXieBUGJPQA9rV8XKi3PBd1yRNxmWxEzi9UwrUVvNG6fDyZ7Ha7cSdqrKr1ZL1ejvd16gE+s6gXXjt5jOxOLu0CS+4TQid/vLlw7EeyqDUvEuGBUaGRT+/fm+9kkaod7GSqNwsvjlGNjZDrDeoUR1MPJoaoREBKkWi5FTVeHSytzjovPUvGC3N+z80g69XxIJVbmYpq4ZFxEE4Zo2H/F+FQlRSFbolpK3TSsZtvpdg5vmZmRTIPtFLZkhuW8PEj+MQn8MgM1A0+DlHkjojbI4EbfDcwN4SOhrnrzJEyR8McDQs82MpaLjOx8FY8qxFCWawqNF+/rvUhE/Y97cZRffoIdarlNRIHBAF2mOM+IY/MN8IvMweTUyXpQKqumjsK7UTGIftykf43KRp0Mv04uinTDz+jZnSLUKf3l+hJwwG0KMr+s98bEoPb1DyX6NbfJjBiP0TF+aQLlXkbHVBvDG3rPVrktYmXYAbhzLg9hRBjI4rRy0OgMxxiHzAagIbAQlzSKURmjCGI8YBBAFMwdDQAGxzhFP+w2DKLIERmZjfGmASKghiEAVAbUwwwksDGJcaoHyBFGEKIl4x46hsWQQQswlUwBYZvNCEZUyQM8CKuUbwPAYXAXKYx+BFEhh9lJtSjqXk6svQhIhBRwxCjGiPaRTPSTyEw2kQtXLIoG30CUZKn3VSrsrcFUmM+OqY9l59OsuK9ecaXIsNCcWksCbDlmYkIK2ilCg2dEX23t654uZFJfSm0xls1fOBbfsG12L9C6rqTbWkTVdS/Vkq/VFmTFzVAojLSv1lldDD3+1fjIhgcsOFBODiIBvP4k3IVnkBTC5Svqroj52n62lAcUwMi+a7IDi8qwa9KJU/VmE9szZmLJslkKnnxOzqrkWJwgb4EmXTVlaCIBN1DVJVeHmr0YNj/KSqF0DJbdA9u5c/8MRl+0MZ1wk28sdl4NvxgVTu0RyE5vdSaRmx7o/C96PVdVyaWW13N4nX9QmXHLavxS17qprL9AqbDyujxvFhnwnqFTbBYjJOrpdpfOncIHK/3hxJXxD1gubZIA2YDP8QCuW7HpRstjXlZT0UsDbEUpPMvmfbndOZbCjsu3Wip0GHd01pNaacmJZ0YWdscRryTSLHebkp7U0h90S20TK5aTamjf9vkS9H7zClL+p1YzidnPjW/ElUhstaF0ZKNamoXkQPvTkUic1y6gxYQboz1Gz7A7aZiXYnu3ZntxBxc9pQMvfPGtmX1qlL562L7Hj3h7AHzSffKeZ1UsjQOB0tM+1fi6FOprDlWjXR4z8Qcqp6Y6oDwaAMNRmOjNwpN/RPPyyeJKg9P4NUYXkitBfaoRYG8MLkgpQnBTOTYcYG2Tlc0uahk0hsgtd0cPrZp9TF9sNXIoA9q+QGz3pnRjtbF48+4JfCs3HDTA9LW+fhBVCeQWW5vVNoJbsVmpnmEXGIxHGEY5HyPsYv8ljUmRI3tM9qoOLbP7mVtQsHWw+QJvMFilzEwr4RmspL7AdIInrxGZ+En2hzjQ2OyvsKOtLZBrNtwtZNfZJqKon8uL9CtrHEwX5VOX8BSIZzL91dL1N8mioFLtJYxNtqXFUozbFqMV/hjZG+K0oP9Q1gAGYfwM+z/esAewghSN/cfump1auFVU1hv8Y6svqc5ya3mfLda1UIbA4yYRZ/R24x9d8SHqCUqR2dPobCt1RtZeMdCz4nFkFPnRdzv36ka3RE8/7vl2XK6gaXN8j1QhvxroOzS+l3BPMLV7uoKfz+6naMkm5BqCzntK1xEIhZGs8DaYETGbHb68eB6EOpWTVOiThoZt3uW6b4Cf+LgDz8Bv383+P3/Nfxn6MfYYfyX6J/nDFh46zZprF3SGA2yhvcFiWL9L/CeNoupdGnP9IEtNf9eaeQG9F+fZr81yZxitsSfWoIfIePn5XMg90dnXMZm1uHorUgm2LMaHO3eu0rXV021xY6wuMY+XBTn6k+GDYjt69v/o3r6D1BLBwhEOt6iWgYAAEATAABQSwECFAAUAAgACACamWZARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAJqZZkBEOt6iWgYAAEATAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA8gYAAAAA" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "false" allowRescaling = "false" /> | ||
Aktuelle Version vom 11. Dezember 2015, 11:46 Uhr
Die folgenden Kapitel werden anhand einer Aufgabe erklärt.
30px Aufgabe
Gegeben ist eine Funktionenschar. Bestimme die Extrempunkte aller Funktionen. Auf welcher Kurve liegen die Extrempunkte? |
Inhaltsverzeichnis |
Funktionenscharen
Berechnung der Extrempunkte:
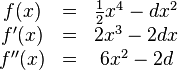
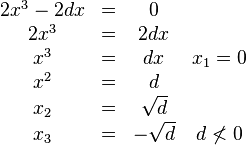
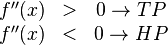
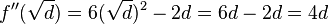
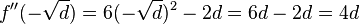
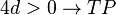 für beide Extrempunkte
für beide Extrempunkte
für 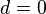 liegt kein Tiefpunkt vor!
liegt kein Tiefpunkt vor!
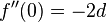
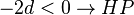 , für
, für 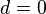 liegt kein Hochpunkt vor!
liegt kein Hochpunkt vor!
Ortskurven
Allgemeine Herleitung einer Ortskurve
Hoch- bzw Tiefpunkt bestimmen
-> Die 1. Ableitung 0 setzen
-> Ergebnis in die 2. Ableitung einsetzen
-> Ergebnis größer 0 -> Tiefpunkt;
Ergebnis kleiner 0 -> Hochpunkt
Ortskurve bestimmen
-> x-Koordinate in die Funktion einsetzen -> Ergebnis bildet die y-Koordinate -> x-Koordinate nach t auflösen -> t Auflösung in y einsetzen -> Lösung = Ortskurvenfunktion
Probe mit Hilfe des GTRs
-> In "Y=" für y1,2,3 für t in der Funktion beliebige Zahlen einsetzen (z.B. 1,2 und 3) -> Ortskurvenfunktion in y4 einsetzen -> Im "Graph" überprüfen, ob die Ortskurve alle Funktionen an derselben Stelle durchläuft
Beispiel Nr. 1
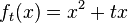
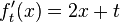
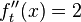
Hoch- bzw Tiefpunkt bestimmen:
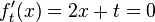
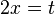
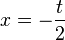
Kurvenverhalten:
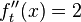
größer als 0 -> Tiefpunkt
Ortskurve bestimmen:
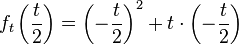
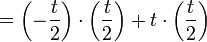
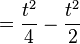
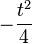
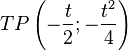
x-Koordinate nach t auflösen:
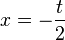
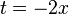
t Auflösung in y einsetzen:
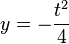
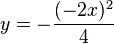
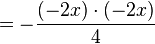
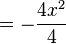
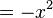 --> Ortskurvenfunktion
--> Ortskurvenfunktion
Probe mit Hilfe des GTRs!
MeJvzm-fsg (Diskussion) 10:21, 11. Dez. 2015 (CET) M.Entenmann
Beispiel Nr. 2
Bestimmen von Ortskurven
Die Koordinaten des Extrempunktes sind 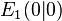 ,
, 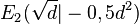 ,
, 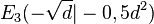
Koordinaten der Extrempunkte einzeln aufschreiben:
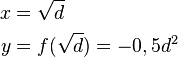
x - Koordinate nach Parameter auflösen:
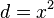
Diesen Parameter in die y - Gleichung einsetzen:
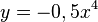
Gleichung der Ortskurve der Extrempunkte: