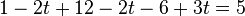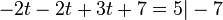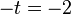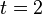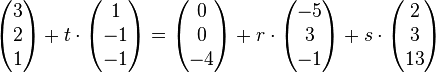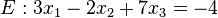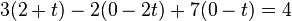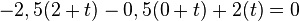Lagebeziehungen zwischen Gerade und Ebene: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
Zeile 88: Zeile 88:
 
-t+3r+3s= &2
 
-t+3r+3s= &2
 
\end{matrix}</math>
 
\end{matrix}</math>
 +
==Aufgaben==
 +
====Nr. 1 Parallelität====
 +
Zeige, dass die Gerade h parallel zur Ebene E ist. <br /><br />
 +
<math>E: \vec x= \left( \begin{matrix} 0\\0\\4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\1 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)</math><br /><br/>
 +
<math>g: \vec x= \left( \begin{matrix} 1\\-1\\-1 \end{matrix}\right)</math><br /><br/>
 +
<popup name="Hinweis">
 +
<math>\left( \begin{matrix} 3\\2\\1 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\-1\\-1 \end{matrix}\right)= \left( \begin{matrix} 0\\0\\-4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\-1 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)</math></popup>
 +
<popup name="Lösung">
 +
0=7 → keine Lösung, daher parallel!
 +
</popup><br /><br />
 +
====Nr. 2 Parallel, identisch oder Schnittpunkt====
 +
Untersuche ob Ebene E und Gerade g sich schneiden. Ist dies nicht der Fall, überprüfe ob g und E identisch sind oder parallel. <br /><br />
 +
a.)<br />
 +
<math>E: \vec x= 3x_{1}-2x_{2}+7x_{3}=-4</math><br /><br />
 +
<math>g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\-2\\-1 \end{matrix}\right)</math><br /><br />
 +
<popup name="Hinweis 1">
 +
Setze Gerade g in Ebene E ein.
 +
</popup><br />
 +
<popup name="Hinweis 2">
 +
<math>E: 3x_{1}-2x_{2}+7x_{3}=-4</math><br />
 +
<math>3(2+t)-2(0-2t)+7(0-t)=4</math>
 +
</popup><br />
 +
<popup name="Lösung">
 +
0=-10 → parallel
 +
</popup><br />
 +
<br />
 +
b.)<br />
 +
<math>E:\vec x=-2,5x_{1}-o,5x_{2}+2x_{3}=0</math><br /><br />
 +
<math>g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\1\\1 \end{matrix}\right)</math><br />br />
 +
<popup name="Hinweis 1">
 +
<math>-2,5(2+t)-0,5(0+t)+2(t)=0</math>
 +
</popup><br />
 +
<popup name="Hinweis 2">
 +
Setze "t" in die Gerade g ein.
 +
</popup><br />
 +
<popup name="Hinweis 3">
 +
t=-5 ; sie sind weder parallel noch identisch
 +
</popup><br />
 +
<popup name="Lösung">
 +
S(-3/-5/-5)
 +
</popup><br />
 +
weitere Aufgaben folgen am 17. September 2016

Version vom 16. September 2016, 16:43 Uhr

Achtung! Diese Seite befindet sich aktuell in Bearbeitung. Die Inhalte sind nicht vollständig!

Inhaltsverzeichnis

Einleitung: Lagebeziehungen zwischen Gerade und Ebene

Gerade und Ebene können verschieden zueinander im dreidimensionalen Raum liegen. Dabei unterscheidet man zwischen diesen drei Möglichkeiten.

1. Möglichkeit: Gerade und Ebene schneiden sich

2. Möglichkeit: Gerade und Ebene verlaufen parallel

3. Möglichkeit: Gerade und Ebene sind identisch

Die Unterschiede der verschiedenen Fälle sind in der Tabelle genau aufgelistet, schau sie dir deshalb gut an.

Datei:Unbenannt 1 - OpenOffice Writer 14.09.2016 174830


Vorgehen

Parameterform

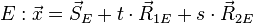
E: \vec x = \vec S_{E} + t \cdot\vec R_{1E} + s \cdot\vec R_{2E}
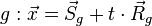
g: \vec x = \vec S_{g} + t \cdot\vec R_{g}

1. Überprüfung "parallel":

→ Skalarprodukt ausrechnen
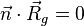
\vec n \cdot \vec R_{g}= 0

Anmerkung: Normalenvektor: 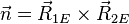\vec n= \vec R_{1E} \times \vec R_{2E} ; das Kreuzprodukt der Richtungsvektoren der Ebene

wenn z.B. t = 5, dann haben die Gerade und Ebene einen Schnittpunkt. Setze nun nur noch t in die Gerade g ein
wenn z.B. 0 = x, dann ist die Gerade und Ebene entweder parallel zueinander oder identisch. Überprüfe dies durch den 2. Schritt

2. Überprüfung "identisch":

→ einfaches LGS erstellen
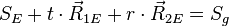
S_{E} + t \cdot\vec R_{1E} + r \cdot\vec R_{2E} = S_{g}
gibt es eine Lösung?
wenn ja, E und g sind identisch.

wenn nein, E und g sind parallel.
→ ist dies der Fall, stelle ein komplettes LGS auf und löse dieses
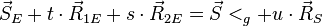
\vec S_{E} + t \cdot\vec R_{1E} + s \cdot\vec R_{2E} = \vec S<_{g} + u \cdot \vec R_{S}

Anmerkung: Löse nach u auf

→ setze u in die Gerade g ein

Koordinatenform

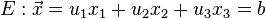
E: \vec x = u_{1}x_{1} + u_{2}x_{2} + u_{3}x_{3} = b
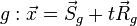
g: \vec x = \vec S_{g} + t \vec R_{g}

Die Gerade g in Ebene E einsetzen:
Die Gerade g Zeilenweise für x1, x2, x3 in Ebene E einsetzen

Schaubild Baum

Beispiele

Beispiel Nr. 1 Koordinatenform:

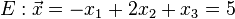
E: \vec x=-x_{1}+2x_{2}+x_{3}=5

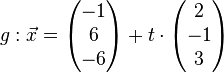
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right)

Die Gerade g Zeilenweise für x1, x2, x3 in Ebene E einsetzen

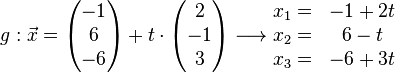
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right)\longrightarrow \begin{matrix} x_{1}= & -1+2t \\ x_{2}= & 6-t \\ x_{3}= & -6+3t \end{matrix}

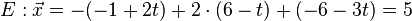
E: \vec x= -(-1+2t) + 2 \cdot (6-t) + (-6-3t) = 5 

          1 - 2t + 12 - 2t - 6 + 3t        = 5

             -2t - 2t + 3t + 7             = 5    | -7

                                        -t = -2   

                                         t = 2

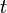t in Gerade g einsetzen:
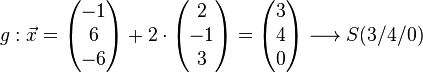
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right) + 2 \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right) = \left( \begin{matrix} 3\\4\\0 \end{matrix}\right) \longrightarrow S(3/4/0)

Beispeil Nr. 2 Parameterform:

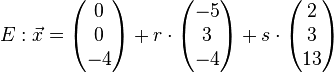
E: \vec x= \left( \begin{matrix} 0\\0\\-4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\-4 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)

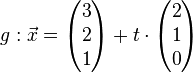
g: \vec x= \left( \begin{matrix} 3\\2\\1 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\1\\0 \end{matrix}\right)

Auf "parallelität" überprüfen:
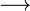\longrightarrow Normalenvektor von Ebene E ausrechnen
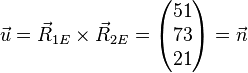
\vec u= \vec R_{1E} \times \vec R_{2E} = \left( \begin{matrix} 51\\73\\21 \end{matrix}\right)= \vec n

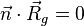
\vec n \cdot \vec R_{g}= 0
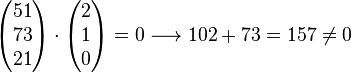
\left( \begin{matrix} 51\\73\\21 \end{matrix}\right) \cdot \left( \begin{matrix} 2\\1\\0 \end{matrix}\right) = 0 \longrightarrow 102+73= 157 \ne 0

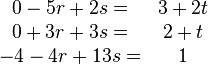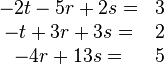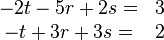
Ergebnis ist ungleich 0, also das LGS lösen: \begin{matrix} 0-5r+2s= &3+2t \\ 0+3r+3s= &2+t \\ -4-4r+13s= &1 \end{matrix}.............. \begin{matrix} -2t-5r+2s= &3 \\ -t+3r+3s= &2 \\ -4r+13s= &5 \end{matrix}.............. \begin{matrix} -2t-5r+2s= &3 \\ -t+3r+3s= &2 \end{matrix}

Aufgaben

Nr. 1 Parallelität

Zeige, dass die Gerade h parallel zur Ebene E ist.

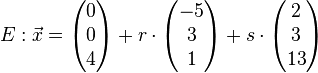
E: \vec x= \left( \begin{matrix} 0\\0\\4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\1 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)

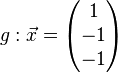
g: \vec x= \left( \begin{matrix} 1\\-1\\-1 \end{matrix}\right)



Nr. 2 Parallel, identisch oder Schnittpunkt

Untersuche ob Ebene E und Gerade g sich schneiden. Ist dies nicht der Fall, überprüfe ob g und E identisch sind oder parallel.

a.)
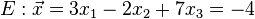
E: \vec x= 3x_{1}-2x_{2}+7x_{3}=-4

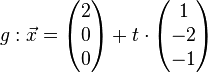
g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\-2\\-1 \end{matrix}\right)





b.)
E:\vec x=-2,5x_{1}-o,5x_{2}+2x_{3}=0

g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\1\\1 \end{matrix}\right)
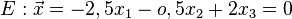
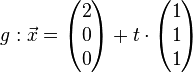
br />





weitere Aufgaben folgen am 17. September 2016

Von „http://fsg.zum.de/index.php?title=Lagebeziehungen_zwischen_Gerade_und_Ebene&oldid=1671“