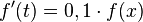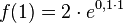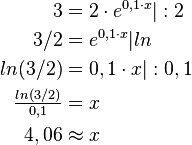Exponentielles Wachstum: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
==Funktionsterm ohne e== | ==Funktionsterm ohne e== | ||
| − | Der Funktionsterm des exponentiellen Wachstums ohne <math>{e}</math> lautet:<br /> | + | Der allgemeine Funktionsterm des exponentiellen Wachstums ohne <math>{e}</math> lautet:<br /> |
<math>{f(x)=a \cdot b^{x}}</math><br /> | <math>{f(x)=a \cdot b^{x}}</math><br /> | ||
<math>{a}</math> steht hierbei für den Anfangsbestand.<br /> | <math>{a}</math> steht hierbei für den Anfangsbestand.<br /> | ||
| − | <math>{b}</math> ist der Wachstums- | + | <math>{b}</math> ist der Wachstums- eziehungsweise Zerfallsfaktor um den der Bestand in einem bestimmten Zeitraum multipliziert wird.<br /> |
===Beispiel=== | ===Beispiel=== | ||
| Zeile 12: | Zeile 12: | ||
Auf einem Bankkonto befinden sich 200 €. Der Zinssatz beträgt 10% (pro Jahr).<br /> | Auf einem Bankkonto befinden sich 200 €. Der Zinssatz beträgt 10% (pro Jahr).<br /> | ||
Der Kontostand kann mit der Funktion<br /> | Der Kontostand kann mit der Funktion<br /> | ||
| − | <math>{f(x)=200 \cdot 1,1^{x}}</math> (<math>{x}</math>in Jahren)<br /> | + | <math>{f(x)=200 \cdot 1,1^{x}}</math> (<math>{x}</math> in Jahren)<br /> |
angegeben werden.<br /> | angegeben werden.<br /> | ||
| Zeile 64: | Zeile 64: | ||
Somit kann die Anzahl der Bakterien (in Millionen) mit der Funktion<br /><math>{f(x)=2 \cdot e^{0,3 \cdot x}}</math><br /> (x in Tagen seit Beobachtungsbeginn) beschrieben werden.<br /><br /><br /><br /><br /><br /><br /> | Somit kann die Anzahl der Bakterien (in Millionen) mit der Funktion<br /><math>{f(x)=2 \cdot e^{0,3 \cdot x}}</math><br /> (x in Tagen seit Beobachtungsbeginn) beschrieben werden.<br /><br /><br /><br /><br /><br /><br /> | ||
| − | |||
{{Aufgabe|Die Anzahl (in 100) der Schafe auf einer Insel kann mit der Funktion <math>{f(t)=2 \cdot e^{0,1 \cdot t}}</math> (t in Jahren) beschrieben werden.<br /> | {{Aufgabe|Die Anzahl (in 100) der Schafe auf einer Insel kann mit der Funktion <math>{f(t)=2 \cdot e^{0,1 \cdot t}}</math> (t in Jahren) beschrieben werden.<br /> | ||
1) Geben Sie die Funktionsgleichung als Differenzialgleichung an!<br /> | 1) Geben Sie die Funktionsgleichung als Differenzialgleichung an!<br /> | ||
Version vom 23. September 2018, 16:00 Uhr
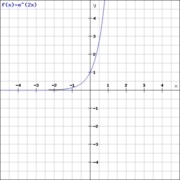
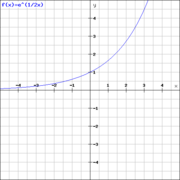
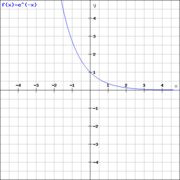
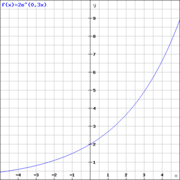
Exponentiell ist ein Wachstum, wenn ein Bestand in gleichen Zeitabständen um einen bestimmten Faktor zu- oder abnimmt. Eine weitere Eigenschaft des exponentiellen Wachstums ist, dass es, wenn es nicht auf der y-Achse verschoben ist, die x-Achse nicht berührt oder schneidet,sondern sich dieser nur annähert.
Exponentialfunktionen können grundsätzlich auf zwei verschiedene Weisen gebildet werden, entweder mit 
oder mit einem anderen Wachstumsfaktor als Basis.
Inhaltsverzeichnis |
Funktionsterm ohne e
Der allgemeine Funktionsterm des exponentiellen Wachstums ohne lautet:
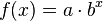
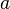steht hierbei für den Anfangsbestand.
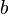ist der Wachstums- eziehungsweise Zerfallsfaktor um den der Bestand in einem bestimmten Zeitraum multipliziert wird.
Beispiel
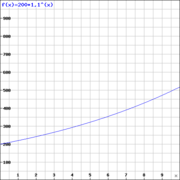
Auf einem Bankkonto befinden sich 200 €. Der Zinssatz beträgt 10% (pro Jahr).
Der Kontostand kann mit der Funktion
(
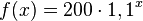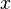in Jahren)
angegeben werden.
30px Aufgabe
2 kg eines radioaktiven Materials haben eine Halbwertszeit von einem Jahr. 2) Wieviel des Materials ist nach 4 Jahren noch übrig? 3) Wann sind noch 22 g des Materials übrig? |
(
Funktionsterm mit e
Der Funktionsterm des exponentiellen Wachstum lautet:
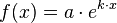
Im Funktionstern steht 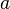für den Anfangsbestand, also den Bestand zum Zeitpunkt 
.
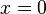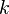steht für die Wachstums- beziehungsweise Zerfallskonstante. Diese bestimmt einerseits, wie "stark" oder "schwach" das Wachstum ist und andererseits ob es sich um Wachstum oder Zerfall handelt.
Die unterschiedlichen Wachstumskonstanten haben ein "stärkeres" oder "schwächeres" exponentielles Wachstum zur Folge.
Für einen exponentiellen Zerfall benötigt man eine negative Wachstumskonstante (Zerfallskonstante).
Differenzialgleichung
Die dazugehörige Differenzialgleichung lautet:
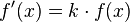
Erklärung:
Die Ableitung des Funktionsterms lautet:
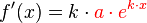
Bis auf die Wachstumskonstante 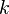ist die Ableitungsfunktion 
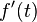identisch mit der Ausgangsfunktion 
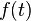, daher kann der identische Teil ersetzt werden:
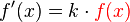
Beispiel
Eine Bakterienkultur besteht zu Beobachtungsbeginn aus 2 Millionen Bakterien. Die Wachstumskonstante lautet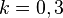 
Somit kann die Anzahl der Bakterien (in Millionen) mit der Funktion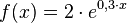
(x in Tagen seit Beobachtungsbeginn) beschrieben werden.
30px Aufgabe
Die Anzahl (in 100) der Schafe auf einer Insel kann mit der Funktion 2) Wie viele Schafe befinden sich nach einem Jahr auf der Insel? 3) Nach wie vielen Jahren befinden sich 300 Schafe auf der Insel? |
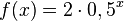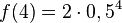
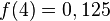
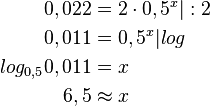
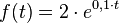(t in Jahren) beschrieben werden.
