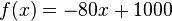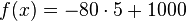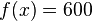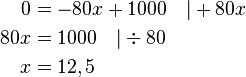Lineares Wachstum: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
| Zeile 1: | Zeile 1: | ||
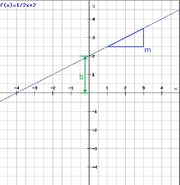
Das lineare Wachstum zeichnet sich dadurch aus, dass es immer dieselbe Änderungsrate, beziehungsweise Steigung, hat. Das heißt in einem bestimmten Zeitraum wird immer dieselbe Menge hinzugefügt oder abgezogen. Dabei sind zwei Eigenschaften veränderbar, und zwar die Änderungsrate <math>{m}</math> und der y-Achsenabschnitt <math>{b}</math>. Daraus folgt die allgemeine Formel:<br /><br /> | Das lineare Wachstum zeichnet sich dadurch aus, dass es immer dieselbe Änderungsrate, beziehungsweise Steigung, hat. Das heißt in einem bestimmten Zeitraum wird immer dieselbe Menge hinzugefügt oder abgezogen. Dabei sind zwei Eigenschaften veränderbar, und zwar die Änderungsrate <math>{m}</math> und der y-Achsenabschnitt <math>{b}</math>. Daraus folgt die allgemeine Formel:<br /><br /> | ||
| + | |||
| + | <!-- Hinweis: Ein Wachstum hat keine Steigung. Wie beziehen sich die Größen m und b auf Größen beim Wachstum? --> | ||
| + | |||
<math>{f(x)=mx+b}</math><br /><br (> | <math>{f(x)=mx+b}</math><br /><br (> | ||
[[Datei:Grafik 1.jpg|rahmenlos|rechts]] Beispiel: | [[Datei:Grafik 1.jpg|rahmenlos|rechts]] Beispiel: | ||
| Zeile 6: | Zeile 9: | ||
<math>{f(x)=\frac{1}{2}x+2}</math><br /> | <math>{f(x)=\frac{1}{2}x+2}</math><br /> | ||
| − | {{Aufgabe|In einer Flasche befindet sich 1 l Wasser. Die Flasche hat ein Loch, durch das gleichmäßig 80 ml pro Minute auslaufen.<br /> | + | {{Aufgabe|1= |
| + | In einer Flasche befindet sich 1 l Wasser. Die Flasche hat ein Loch, durch das gleichmäßig 80 ml pro Minute auslaufen.<br /> | ||
1) Stellen Sie dazu eine Funktionsgleichung auf!<br /> | 1) Stellen Sie dazu eine Funktionsgleichung auf!<br /> | ||
| − | <popup name="Lösung"> | + | 2) Wieviel Wasser befindet sich nach 5 Minuten noch in der Flasche?<br /> |
| + | 3) Wann ist die Flasche leer? | ||
| + | }} | ||
| + | |||
| + | <popup name="Lösung 1)"> | ||
<math>{f(x)=-80x+1000}</math> | <math>{f(x)=-80x+1000}</math> | ||
</popup> | </popup> | ||
| − | + | ||
| − | <popup name=" | + | <popup name="Lösung2 )"> |
<math>{f(x)=-80 \cdot 5+1000}</math><br /> | <math>{f(x)=-80 \cdot 5+1000}</math><br /> | ||
<math>{f(x)=600}</math><br /> | <math>{f(x)=600}</math><br /> | ||
Nach 5 Minuten befinden sich noch 600 ml in der Flasche. | Nach 5 Minuten befinden sich noch 600 ml in der Flasche. | ||
</popup> | </popup> | ||
| − | + | ||
| − | <popup name="Lösung"> | + | <popup name="Lösung 3)"> |
<math> \begin{align} | <math> \begin{align} | ||
0 &=-80x+1000 \quad |+80x \\ | 0 &=-80x+1000 \quad |+80x \\ | ||
| Zeile 24: | Zeile 32: | ||
x &=12,5 \end{align}</math><br /><br /> | x &=12,5 \end{align}</math><br /><br /> | ||
Nach 12,5 Minuten ist die Flasche leer. | Nach 12,5 Minuten ist die Flasche leer. | ||
| − | </popup> | + | </popup> |
Version vom 3. November 2018, 19:27 Uhr
Das lineare Wachstum zeichnet sich dadurch aus, dass es immer dieselbe Änderungsrate, beziehungsweise Steigung, hat. Das heißt in einem bestimmten Zeitraum wird immer dieselbe Menge hinzugefügt oder abgezogen. Dabei sind zwei Eigenschaften veränderbar, und zwar die Änderungsrate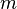 
und der y-Achsenabschnitt 
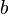. Daraus folgt die allgemeine Formel:
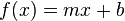
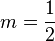
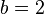
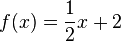
30px Aufgabe
In einer Flasche befindet sich 1 l Wasser. Die Flasche hat ein Loch, durch das gleichmäßig 80 ml pro Minute auslaufen. |
