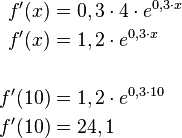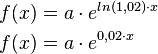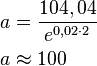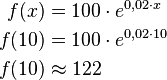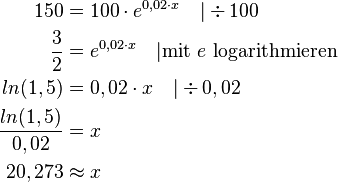Exponentielles Wachstum: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | + | Beim exponentiellen Wachstum ist die Änderungsrate propertional zum Bestand.<br /><br /> | |
| + | |||
| + | Das bedeutet, dass die Änderungsrate entsprechend dem Besatnd steigt, also umso größer wird, je größer der Bestand wird.<br /> | ||
| + | Der Graph einer exponentiellen Wachstumsfunktion hat die Eigenschaft, sofern er nicht verschoben oder gespiegelt ist, die x-Achse niemals zu schneiden, sondern sich dieser im negativen Bereich nur anzunähern.<br /> | ||
| + | |||
<!-- Ein Wachstum kann nicht auf einer Achse verschoben sein!!! --> | <!-- Ein Wachstum kann nicht auf einer Achse verschoben sein!!! --> | ||
| Zeile 8: | Zeile 12: | ||
<math>{f(x)=a \cdot e^{k \cdot x}}</math><br /><br /> | <math>{f(x)=a \cdot e^{k \cdot x}}</math><br /><br /> | ||
Dabei steht <math>{a}</math> für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{x=0}</math>.<br /> | Dabei steht <math>{a}</math> für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{x=0}</math>.<br /> | ||
| − | Die Eurlerische Zahl <math>{e}</math> | + | Die Eurlerische Zahl <math>{e}</math> erfüllt in dieser Schreibweise die Aufgabe des Wachstumsfaktors.<br /> |
<!-- FALSCH. Die Wachstumskonstantze ist k - siehe nächste Zeile. --> | <!-- FALSCH. Die Wachstumskonstantze ist k - siehe nächste Zeile. --> | ||
| − | <math>{k}</math> ist die sogenannte Wachstumskonstante, die für die Umwandlung der | + | <math>{k}</math> ist die sogenannte Wachstumskonstante, die für die Umwandlung der Scheibweise ohne <math>{e}</math> in die Schreibweise mit <math>{e}</math> als Basis von Bedeutung ist. |
| − | ==Umwandlung der | + | ==Umwandlung der Scheibweise ohne <math>{e}</math> in die Schreibweise mit <math>{e}</math> als Basis== |
<!-- Es gibt keine alte und neue Schreibweise. Es gibt eine Schreibweise als Exponentialfunktion, und eine als Exponentialfunktion mit der Basis e. --> | <!-- Es gibt keine alte und neue Schreibweise. Es gibt eine Schreibweise als Exponentialfunktion, und eine als Exponentialfunktion mit der Basis e. --> | ||
| − | Exponentialfunktionen können grundsätzlich auf zwei verschiedene Weisen gebildet werden, entweder | + | Exponentialfunktionen können grundsätzlich auf zwei verschiedene Weisen gebildet werden, entweder mit <math>{e}</math> als Basis, oder ohne <math>{e}</math>.<br /><br /> |
| − | + | Die allgemeine Form lautet:<br /> | |
<math>{f(x)=a \cdot b^{x}}</math><br /> | <math>{f(x)=a \cdot b^{x}}</math><br /> | ||
| + | Eine Wachstumsfunktion in der Schreibweise ohne <math>{e}</math> lässt sich leichter aufstellen, da man den Wachstumsfaktor <math>{b}</math> aus einer gegebenen prozentualen Zunahme bilden kann. Dafür muss man die prozentuale Zunahme mit 1 addieren.<br /> | ||
| + | Ist die prozentuale Zunahme beispielsweise 25%, so beträgt <math>{b}</math> folglich 1,25. | ||
<!-- Was ist hier der Vorteil? Hinweis auf Wachstumsrate um x Prozent, was sich in b zeigt -> Formel angeben. --> | <!-- Was ist hier der Vorteil? Hinweis auf Wachstumsrate um x Prozent, was sich in b zeigt -> Formel angeben. --> | ||
Version vom 24. November 2018, 20:37 Uhr
Beim exponentiellen Wachstum ist die Änderungsrate propertional zum Bestand.
Das bedeutet, dass die Änderungsrate entsprechend dem Besatnd steigt, also umso größer wird, je größer der Bestand wird.
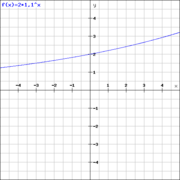
Der Graph einer exponentiellen Wachstumsfunktion hat die Eigenschaft, sofern er nicht verschoben oder gespiegelt ist, die x-Achse niemals zu schneiden, sondern sich dieser im negativen Bereich nur anzunähern.
Inhaltsverzeichnis |
Funktionsterm
Für Exponentialfunktionen lautet die allgemeine Form:
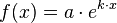
Dabei steht 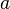 für den Anfangsbestand, also den Bestand zum Zeitpunkt
für den Anfangsbestand, also den Bestand zum Zeitpunkt 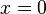 .
.
Die Eurlerische Zahl  erfüllt in dieser Schreibweise die Aufgabe des Wachstumsfaktors.
erfüllt in dieser Schreibweise die Aufgabe des Wachstumsfaktors.
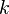 ist die sogenannte Wachstumskonstante, die für die Umwandlung der Scheibweise ohne
ist die sogenannte Wachstumskonstante, die für die Umwandlung der Scheibweise ohne  in die Schreibweise mit
in die Schreibweise mit  als Basis von Bedeutung ist.
als Basis von Bedeutung ist.
Umwandlung der Scheibweise ohne  in die Schreibweise mit
in die Schreibweise mit  als Basis
als Basis
Exponentialfunktionen können grundsätzlich auf zwei verschiedene Weisen gebildet werden, entweder mit  als Basis, oder ohne
als Basis, oder ohne  .
.
Die allgemeine Form lautet:
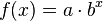
Eine Wachstumsfunktion in der Schreibweise ohne  lässt sich leichter aufstellen, da man den Wachstumsfaktor
lässt sich leichter aufstellen, da man den Wachstumsfaktor 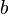 aus einer gegebenen prozentualen Zunahme bilden kann. Dafür muss man die prozentuale Zunahme mit 1 addieren.
aus einer gegebenen prozentualen Zunahme bilden kann. Dafür muss man die prozentuale Zunahme mit 1 addieren.
Ist die prozentuale Zunahme beispielsweise 25%, so beträgt 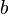 folglich 1,25.
folglich 1,25.
Diese kann in eine Exponentialfunktion mit  umgewandelt werden. Mit
umgewandelt werden. Mit  lautet die allgemeine Formel:
lautet die allgemeine Formel:
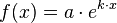
Bei der alten Schreibweise fehlt als Unbekannte im Vergleich zu der neuen nur die Wachstumskonstante 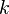 .
.
Ausrechnen lässt sich die Wachstumskonstante, indem man beide Formen gleichsetzt:
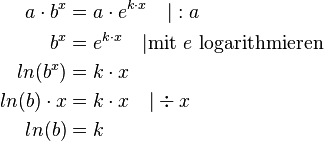
Um die alte Schreibweise in die neue umzuwandeln muss man also nur den natürlichen Logarithmus des ursprünglichen Wachstumsfaktors bilden und das Ergebnis als Wachstumskonstante im Exponent mit 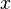 multiplizieren.
multiplizieren.
Beispiel
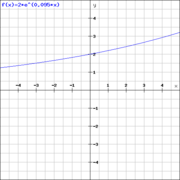
Ein Anfangsbestand von 2 vermehrt sich in bestimmten Abständen um 10%.
Alte Schreibweise:
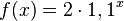
Neue Schreibweise:
1. Wachstumskonstante berechnen:
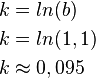
2. Funktionsgleichung aufstellen:
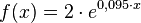
30px Aufgabe
Ein Anfangsbestand von 1 vermehrt sich in bestimmten Abständen um 50%. |
Anfangsbestand berechnen
Wenn der Anfangsbestand unbekannt ist müssen alle anderen Werte gegeben sein, auch ein y-Wert.
Um 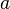 auszurechnen muss die Funktionsgleichung umgeformt werden.
auszurechnen muss die Funktionsgleichung umgeformt werden.
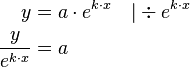
Beispiel
Es ist gegeben, dass ein Graph mit der Wachstumskonstante 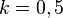 an der Stelle
an der Stelle 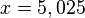 eine Höhe von
eine Höhe von 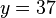 hat.
hat.
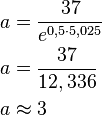
30px Aufgabe
Es ist gegeben, dass ein Graph mit der Wachstumskonstante |
Wachstumsgeschwindigkeit berechnen
Um die Wachstumsgeschwindigkeit zu berechnen, muss man die Ableitung bilden.
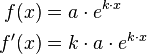
Mit der ableitungsfunktion lässt sich die Wachstumsgeschwindigkeit an jeder beliebiger Stelle des Graphen berechen.
Beispiel
Gegeben ist die Funktion
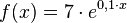
Die dazugehörige Ableitungsfunktion lautet:
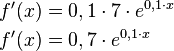
30px Aufgabe
Gegeben ist die Funktion |
Übungsaufgabe
30px Aufgabe
Eine Bank bietet 2% (jährlich) Zinsen. a)Geben Sie, so weit möglich, die Funktionsgleichung in der neuen Schreibweise an! b)Wie hoch war der Kontostand zu Beobachtungsbeginn, wenn nach zwei Jahren 104,04 € auf dem Konto sind? c)Wieviel Geld wird nach 10 Jahren auf dem Konto sein? d)Wann befinden sich 150 € auf dem Konto? |
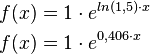
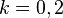 an der Stelle
an der Stelle 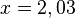 eine Höhe von
eine Höhe von 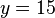 hat.
Bestimmen Sie den Anfangsbestand
hat.
Bestimmen Sie den Anfangsbestand 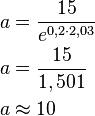
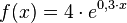
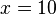 !
!