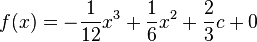Kurvenanpassung: Unterschied zwischen den Versionen
(→Vorgehensweise) |
(→Anwendungsbeispiel) |
||
| Zeile 40: | Zeile 40: | ||
Der GTR gibt dann folgendes Ergebnis aus:<br /> | Der GTR gibt dann folgendes Ergebnis aus:<br /> | ||
<math>a= -\frac{1}{12}; b= \frac{1}{6}; c= \frac{2}{3}; d=0</math><br /> | <math>a= -\frac{1}{12}; b= \frac{1}{6}; c= \frac{2}{3}; d=0</math><br /> | ||
| − | Jetzt muss man nur noch die Buchstaben durch die Zahlen ersetzen:<br /> | + | |
| + | Jetzt muss man nur noch die Buchstaben durch die Zahlen ersetzen.<br /> | ||
| + | Die endgültige Funktion lautet:<br /> | ||
<math>f(x)= -\frac{1}{12} x^3 + \frac{1}{6} x^2 + \frac{2}{3} c + 0</math><br /> | <math>f(x)= -\frac{1}{12} x^3 + \frac{1}{6} x^2 + \frac{2}{3} c + 0</math><br /> | ||
Version vom 10. März 2012, 15:31 Uhr
Vorgehensweise
Als Erstes muss man die Bedingungen die das Schaubild aufweist herausfinden.
Dazu gehören Koordinaten, Extrempunkte und Nullpunkte.
Anschließend muss ein Graph des richtigen Grades gefunden werden. Falls dieser nicht gegeben ist muss man ihn raten.
Anschließend wird die Normalfunktion aufgeschrieben. Z.B.: 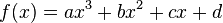
Die gegebenen Bedinungen werden in die Gleichung eingesetzt.
Anschließend kann man das Gleichungssystem in die Form des Gauß-Algorithmus umschreiben und mit dem GTR lösen.
Anwendungsbeispiel
Gegebene Eigenschaften:
1) Der Graph ist eine ganzrationale Funktion des 3. Grades.
2) Der Graph verläuft durch den Ursprung.
3) Er hat die Nullstellen x1 = -2 und x2 = 4.
4) An der Stelle x = 2 hat die Tangente die Steigung m = -2.
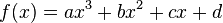
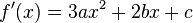
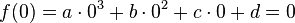
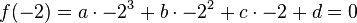
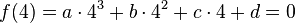
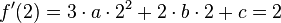
Daraus Folgt:
| a | b | c | d | |
|---|---|---|---|---|
| -8 | 4 | -2 | 1 | 0 |
| 64 | 16 | 4 | 1 | 0 |
| 48 | 8 | 1 | 0 | -2 |
Der GTR gibt dann folgendes Ergebnis aus:
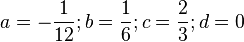
Jetzt muss man nur noch die Buchstaben durch die Zahlen ersetzen.
Die endgültige Funktion lautet: