Ebenengleichungen: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
| Zeile 20: | Zeile 20: | ||
<br /> | <br /> | ||
Liegt M(2/2/2) in E?<br /> | Liegt M(2/2/2) in E?<br /> | ||
| − | => <math> 2+2+2-4=-2</math> | + | => <math> 2+2+2-4=-2 \not= 0 </math> <br /> |
M liegt nicht auf E | M liegt nicht auf E | ||
Aktuelle Version vom 19. Juni 2012, 07:59 Uhr
Es gibt verschiedene Möglichkeiten Ebenen durch eine Gleichung darzustellen.
Koordinatengleichung:
Eine Gleichung der Form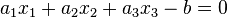 
beschreibt eine Ebene im Raum
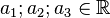- Koeffizienten
=> Setzen wir für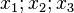 
Zahlen 
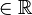ein, dass die Gleichung erfüllt ist, so erhalten wir Punkte dieser Ebene.
Beispiel: Dreieck im Würfel:
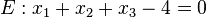
Liegt A(4/0/0) in E?
=> 4+0+0-4=0 richtig A liegt auf der Ebene E
Liegt M(2/2/2) in E?
=> 
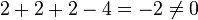
M liegt nicht auf E
