Lineare Unabhängigkeit von Vektoren: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(Die Seite wurde neu angelegt: „===Lineare Abhängigkeit zweier Vektoren=== Definition: Vektoren sind voneinander abhängig, wenn sie Vielfache voneinander sind. Bsp. <math> \vec p= \left( \b…“) |
(→Lineare Unabhängigkeit dreier oder mehrerer Vektoren) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
<math> \left( \begin{matrix} -2\\6\\6 \end{matrix}\right) = t\cdot\left( \begin{matrix} -1\\3\\2 \end{matrix}\right) </math> | <math> \left( \begin{matrix} -2\\6\\6 \end{matrix}\right) = t\cdot\left( \begin{matrix} -1\\3\\2 \end{matrix}\right) </math> | ||
| − | |||
| + | <math> \left( \begin{matrix}t= -2\\ t=2\\t= -3 \end{matrix}\right) </math> | ||
| + | --> <math> \vec p </math> und <math> \vec q </math> sind nicht linear abhängig | ||
| + | ===Lineare Unabhängigkeit dreier oder mehrerer Vektoren=== | ||
| − | + | Prüfe ob <math> \vec p= \left( \begin{matrix} 1\\3\\-2\end{matrix}\right) </math> linear abhängig ist von <math> \vec q= \left( \begin{matrix} 2\\2\\2 \end{matrix}\right) </math> und <math> \vec u= \left( \begin{matrix} -2\\6\\1\end{matrix}\right)</math> | |
| + | |||
| + | <math> \left( \begin{matrix} 1\\3\\-2\end{matrix}\right) </math> = <math> r\cdot \left( \begin{matrix} 2\\2\\2 \end{matrix}\right) </math> + <math> s\cdot \left( \begin{matrix} -2\\6\\1\end{matrix}\right)</math> | ||
| + | |||
| + | 1.Möglichkeit: Vektoren in ein Lineares Gleichungssystem | ||
| + | |||
| + | <math>\begin{matrix} | ||
| + | 1.&2r&-&2s&=&1\\ | ||
| + | 2.&2r&+&6s&=&3\\ | ||
| + | 3.&2r&+&1s&=&-2 | ||
| + | \end{matrix}</math> | ||
| + | |||
| + | 3.<math> s= -2-2r </math> | ||
| + | 3 in 2. | ||
| + | <math>\begin{matrix} | ||
| + | &2r&+&6(-2-2r)&=&3\\ | ||
| + | &10r&=&-15 | ||
| + | &r&=& \frac {-3\over 2} | ||
| + | \end{matrix}</math> | ||
Aktuelle Version vom 19. Juni 2012, 08:02 Uhr
Lineare Abhängigkeit zweier Vektoren
Definition: Vektoren sind voneinander abhängig, wenn sie Vielfache voneinander sind.
Bsp.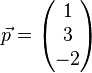 
--> 
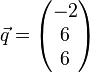
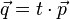
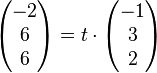
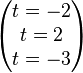
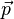und 
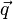sind nicht linear abhängig
Lineare Unabhängigkeit dreier oder mehrerer Vektoren
Prüfe ob 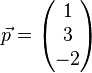linear abhängig ist von 
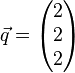und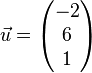 
= 
+ 
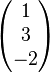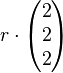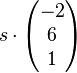
1.Möglichkeit: Vektoren in ein Lineares Gleichungssystem
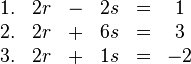
3.
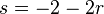3 in 2.
Fehler beim Parsen(Syntaxfehler): \begin{matrix} &2r&+&6(-2-2r)&=&3\\ &10r&=&-15 &r&=& \frac {-3\over 2} \end{matrix}
