Lagebeziehungen zwischen Ebene und Ebene: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Beide Ebenen in Koordinatengleichung gegeben)
 
(7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 7: Zeile 7:
 
Für jeden Punkt gibt es ein eigenes Kapitel. Du sollst aber wissen, dass man den zweiten und dritten Punkt immer auf den ersten zurückführen kann, indem eine/beide Ebene(n) in eine Koordinatengleichung umgewandelt werden. Wie das geht, ist in einem anderen Abschnitt beschrieben.}}
 
Für jeden Punkt gibt es ein eigenes Kapitel. Du sollst aber wissen, dass man den zweiten und dritten Punkt immer auf den ersten zurückführen kann, indem eine/beide Ebene(n) in eine Koordinatengleichung umgewandelt werden. Wie das geht, ist in einem anderen Abschnitt beschrieben.}}
  
−
== Beide Ebenen in Koordinatengleichuing gegeben ==
+
== Beide Ebenen in Koordinatengleichung gegeben ==
  
 
{{Aufgabe|Welche der Ebenen E<sub>1</sub>, E<sub>2</sub>, E<sub>3</sub>, E<sub>4</sub>  sind zueinander parallel?}}
 
{{Aufgabe|Welche der Ebenen E<sub>1</sub>, E<sub>2</sub>, E<sub>3</sub>, E<sub>4</sub>  sind zueinander parallel?}}
Zeile 15: Zeile 15:
 
<math>E_2:-x_1 + 2x_2 -3x_3 = 4</math>
 
<math>E_2:-x_1 + 2x_2 -3x_3 = 4</math>
  
−
<math>E_2:-6 x_1 + 4x_2 -2x_3 = 1</math>
+
<math>E_3:-6 x_1 + 4x_2 -2x_3 = 1</math>
  
 
<math>E_4:-3 x_1 + 2x_2 -x_3 = -4</math>
 
<math>E_4:-3 x_1 + 2x_2 -x_3 = -4</math>
  
 
{{Lösung versteckt mit Rand|
 
{{Lösung versteckt mit Rand|
−
1=Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E<sub>1</sub> und E<sub>3</sub>), sonst sind sie identisch (Ebenen E<sub>1</sub> und E<sub>4</sub>). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E<sub>2</sub> mit allen anderen Ebenen.
+
1=Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E<sub>1</sub> und E<sub>3</sub>), sonst sind sie identisch (Ebenen E<sub>1</sub> und E<sub>4</sub>). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E<sub>2</sub> mit allen anderen Ebenen).
  
 
<math> \vec n_1= \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) </math>,
 
<math> \vec n_1= \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) </math>,
Zeile 27: Zeile 27:
 
<math> \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) </math>.
 
<math> \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) </math>.
  
−
<math> -2 \cdot \vec n_1= -2 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \vec n_2= \left( \begin{matrix} -1\\2\\-3\end{matrix}\right)</math>, aber <math>E_1:3x_1 - 2x_2 +x_3 = 4 \neq E_2:-6 x_1 + 4x_2 -2x_3 = 1</math>
+
<math> -2 \cdot \vec n_1= -2 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -6\\4\\-2\end{matrix}\right) = \vec n_3</math>, aber <math>-2 \cdot 4 \neq 1</math>
  
−
<math> -1 \cdot \vec n_1= -1 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right)</math>
+
<math> -1 \cdot \vec n_1= -1 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) = \vec n_4</math>, aber <math>-1 \cdot 4 = -4</math>
 +
}}
  
 +
Somit lässt sich eine Vorgehensweise verallgemeinern, mit der man die Lage zweier Ebenen untersuchen kann, indem man die Normalenvektoren untersucht und eventuell noch die gesamte Gleichung betrachtet.
  
 +
{{Aufgabe|Erstelle ein Baumdiagramm als Arbeitsanweisung zur Untersuchung der Lage zweier Ebenen, die durch eine Koordinatengleichung gegeben sind.}}
 +
 +
{{Lösung versteckt mit Rand|
 +
1=Lösung:
 +
 +
<graphviz>
 +
digraph G {
 +
Normalenvektorenla [shape=box];
 +
Normalenvektorenla -> Ebenengleichungenidentisch; /* [label="ja"] /*
 +
Normalenvektorenla -> Ebenenschneidensich; /* [label="nein"] /*
 +
Ebenengleichungenidentisch -> Ebenensindidentisch; /* [label="ja"]/*
 +
Ebenengleichungenidentisch -> Ebenensindparallel; /* [label="nein"]/*
 +
}
 +
</graphviz>
 
}}
 
}}
 +
 +
{{Übung|1=Gegeben ist die Ebene E<sub>1</sub>: 3x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>=6.
 +
 +
a) Bestimme die Lage der Ebene E<sub>2</sub>:9x<sub>1</sub>+4<sub>2</sub>+x<sub>3</sub>=36 zur Ebene E<sub>1</sub>.
 +
 +
b) Bestimme die Parameter a und b so, dass die Ebene E<sub>3</sub>:ax<sub>1</sub>-8x<sub>2</sub>-4x<sub>3</sub>=b parallel zu E<sub>1</sub> ist.}}
 +
 +
{{Lösung versteckt mit Rand|
 +
1=Lösung:
 +
 +
}}
 +
 +
== Beide Ebenen in Parameterform gegeben ==

Aktuelle Version vom 25. September 2012, 13:11 Uhr

Mathematik-digital Pfeil-3d.png
Lernpfad

Im Laufe dieses Lernpfades sollst du die Lage zweier Ebenen untersuchen können. Dieses Thema ist deshalb so komplex, da Ebenen in - vereinfacht - zwei Darstellungsformen gegeben sein können:

  • beide Ebenen in Koordinatengleichung,
  • beide Ebenen in Parameterform,
  • eine Ebene in Parameterform, eine Ebene in Koordinatengleichung.

Für jeden Punkt gibt es ein eigenes Kapitel. Du sollst aber wissen, dass man den zweiten und dritten Punkt immer auf den ersten zurückführen kann, indem eine/beide Ebene(n) in eine Koordinatengleichung umgewandelt werden. Wie das geht, ist in einem anderen Abschnitt beschrieben.

Beide Ebenen in Koordinatengleichung gegeben

30px   Aufgabe

Welche der Ebenen E1, E2, E3, E4 sind zueinander parallel?

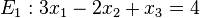
E_1:3x_1 - 2x_2 +x_3 = 4

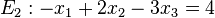
E_2:-x_1 + 2x_2 -3x_3 = 4

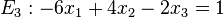
E_3:-6 x_1 + 4x_2 -2x_3 = 1

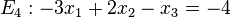
E_4:-3 x_1 + 2x_2 -x_3 = -4

Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E1 und E3), sonst sind sie identisch (Ebenen E1 und E4). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E2 mit allen anderen Ebenen).

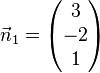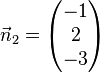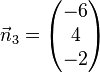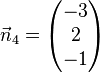\vec n_1= \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) , \vec n_2= \left( \begin{matrix} -1\\2\\-3\end{matrix}\right) , \vec n_3= \left( \begin{matrix} -6\\4\\-2\end{matrix}\right) , \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) .

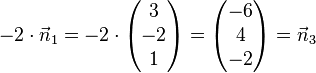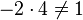
-2 \cdot \vec n_1= -2 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -6\\4\\-2\end{matrix}\right) = \vec n_3, aber -2 \cdot 4 \neq 1

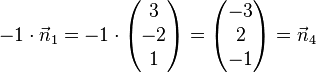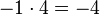
-1 \cdot \vec n_1= -1 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) = \vec n_4, aber -1 \cdot 4 = -4


Somit lässt sich eine Vorgehensweise verallgemeinern, mit der man die Lage zweier Ebenen untersuchen kann, indem man die Normalenvektoren untersucht und eventuell noch die gesamte Gleichung betrachtet.

30px   Aufgabe

Erstelle ein Baumdiagramm als Arbeitsanweisung zur Untersuchung der Lage zweier Ebenen, die durch eine Koordinatengleichung gegeben sind.

Lösung:

<graphviz> digraph G { Normalenvektorenla [shape=box]; Normalenvektorenla -> Ebenengleichungenidentisch; /* [label="ja"] /* Normalenvektorenla -> Ebenenschneidensich; /* [label="nein"] /* Ebenengleichungenidentisch -> Ebenensindidentisch; /* [label="ja"]/* Ebenengleichungenidentisch -> Ebenensindparallel; /* [label="nein"]/* }

</graphviz>


Hand.gif   Übung

Gegeben ist die Ebene E1: 3x1+2x2+x3=6.

a) Bestimme die Lage der Ebene E2:9x1+42+x3=36 zur Ebene E1.

b) Bestimme die Parameter a und b so, dass die Ebene E3:ax1-8x2-4x3=b parallel zu E1 ist.

Lösung:


Beide Ebenen in Parameterform gegeben

Von „http://fsg.zum.de/index.php?title=Lagebeziehungen_zwischen_Ebene_und_Ebene&oldid=751“