|
Lernpfad
|
Im Laufe dieses Lernpfades sollst du die Lage zweier Ebenen untersuchen können. Dieses Thema ist deshalb so komplex, da Ebenen in - vereinfacht - zwei Darstellungsformen gegeben sein können:
- beide Ebenen in Koordinatengleichung,
- beide Ebenen in Parameterform,
- eine Ebene in Parameterform, eine Ebene in Koordinatengleichung.
Für jeden Punkt gibt es ein eigenes Kapitel. Du sollst aber wissen, dass man den zweiten und dritten Punkt immer auf den ersten zurückführen kann, indem eine/beide Ebene(n) in eine Koordinatengleichung umgewandelt werden. Wie das geht, ist in einem anderen Abschnitt beschrieben.
|
|
Beide Ebenen in Koordinatengleichung gegeben
|
Welche der Ebenen E1, E2, E3, E4 sind zueinander parallel?
|
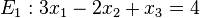
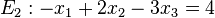
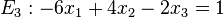
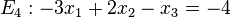
[Lösung anzeigen][Lösung ausblenden]
Somit lässt sich eine Vorgehensweise verallgemeinern, mit der man die Lage zweier Ebenen untersuchen kann, indem man die Normalenvektoren untersucht und eventuell noch die gesamte Gleichung betrachtet.
|
Erstelle ein Baumdiagramm als Arbeitsanweisung zur Untersuchung der Lage zweier Ebenen, die durch eine Koordinatengleichung gegeben sind.
|
[Lösung anzeigen][Lösung ausblenden]
Lösung:
<graphviz>
digraph G {
Normalenvektorenla [shape=box];
Normalenvektorenla -> Ebenengleichungenidentisch; /* [label="ja"] /*
Normalenvektorenla -> Ebenenschneidensich; /* [label="nein"] /*
Ebenengleichungenidentisch -> Ebenensindidentisch; /* [label="ja"]/*
Ebenengleichungenidentisch -> Ebenensindparallel; /* [label="nein"]/*
}
</graphviz>
 Übung
Gegeben ist die Ebene E1: 3x1+2x2+x3=6.
a) Bestimme die Lage der Ebene E2:9x1+42+x3=36 zur Ebene E1.
b) Bestimme die Parameter a und b so, dass die Ebene E3:ax1-8x2-4x3=b parallel zu E1 ist.
|
[Lösung anzeigen][Lösung ausblenden]
Beide Ebenen in Parameterform gegeben
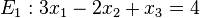
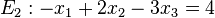
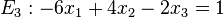
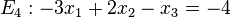
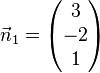 ,
,
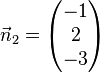 ,
,
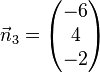 ,
,
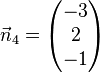 .
.
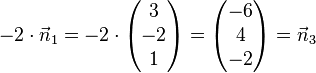 , aber
, aber 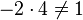
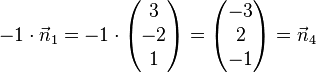 , aber
, aber