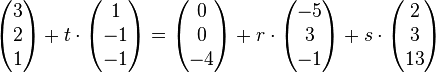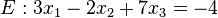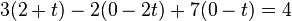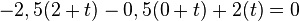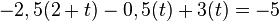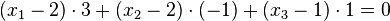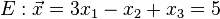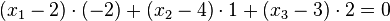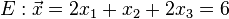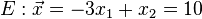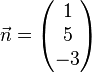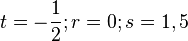Lagebeziehungen zwischen Gerade und Ebene: Unterschied zwischen den Versionen

Aus Friedrich-Schiller-Gymnasium
Wechseln zu: Navigation, Suche
(→‎Einleitung: Lagebeziehungen zwischen Gerade und Ebene)
Zeile 8: Zeile 8:
 
3. Möglichkeit: Gerade und Ebene sind <u>liegen ineinander</u><br /><br />
 
3. Möglichkeit: Gerade und Ebene sind <u>liegen ineinander</u><br /><br />
  
−
Die Unterschiede der verschiedenen Fälle sind in der Tabelle genau aufgelistet, schau sie dir deshalb gut an.<br />
+
Wie du die verschiedenen Fälle mit Hilfe eines LGS unterscheiden kannst, ist in der Tabelle genau aufgelistet. Schau sie dir deshalb gut an.<br />
 
[[Bild:Gfs Lagebeziehungen Gerade Ebene.odt - OpenOffice Writer 21.11.2016 170233.bmp.jpg|Lagebeziehungen Gerade Ebene]]<br />
 
[[Bild:Gfs Lagebeziehungen Gerade Ebene.odt - OpenOffice Writer 21.11.2016 170233.bmp.jpg|Lagebeziehungen Gerade Ebene]]<br />
 
<br />
 
<br />
 +
 
== Vorgehen ==
 
== Vorgehen ==
 
====  Parameterform ====
 
====  Parameterform ====

Version vom 25. Januar 2017, 13:07 Uhr

Inhaltsverzeichnis

Einleitung: Lagebeziehungen zwischen Gerade und Ebene

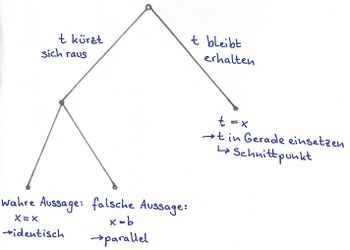
Gerade und Ebene können verschieden zueinander im dreidimensionalen Raum liegen. Dabei unterscheidet man zwischen diesen drei Möglichkeiten.

1. Möglichkeit: Gerade und Ebene schneiden sich

2. Möglichkeit: Gerade und Ebene verlaufen parallel

3. Möglichkeit: Gerade und Ebene sind liegen ineinander

Wie du die verschiedenen Fälle mit Hilfe eines LGS unterscheiden kannst, ist in der Tabelle genau aufgelistet. Schau sie dir deshalb gut an.
Lagebeziehungen Gerade Ebene

Vorgehen

Parameterform

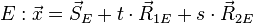
E: \vec x = \vec S_{E} + t \cdot\vec R_{1E} + s \cdot\vec R_{2E}
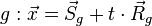
g: \vec x = \vec S_{g} + t \cdot\vec R_{g}

1. Überprüfung "parallel":

→ Skalarprodukt ausrechnen
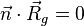
\vec n \cdot \vec R_{g}= 0

Anmerkung: Normalenvektor: 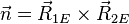\vec n= \vec R_{1E} \times \vec R_{2E} ; das Kreuzprodukt der Richtungsvektoren der Ebene

wenn z.B. t = 5, dann haben die Gerade und Ebene einen Schnittpunkt. Setze nun nur noch t in die Gerade g ein
wenn z.B. 0 = x, dann ist die Gerade und Ebene entweder parallel zueinander oder identisch. Überprüfe dies durch den 2. Schritt

2. Überprüfung "identisch":

→ einfaches LGS erstellen
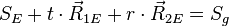
S_{E} + t \cdot\vec R_{1E} + r \cdot\vec R_{2E} = S_{g}
gibt es eine Lösung?
wenn ja, E und g sind identisch.

wenn nein, E und g sind parallel.
→ ist dies der Fall, stelle ein komplettes LGS auf und löse dieses
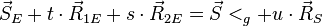
\vec S_{E} + t \cdot\vec R_{1E} + s \cdot\vec R_{2E} = \vec S<_{g} + u \cdot \vec R_{S}

Anmerkung: Löse nach u auf

→ setze u in die Gerade g ein

Koordinatenform

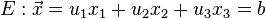
E: \vec x = u_{1}x_{1} + u_{2}x_{2} + u_{3}x_{3} = b
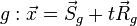
g: \vec x = \vec S_{g} + t \vec R_{g}

Die Gerade g in Ebene E einsetzen:
Die Gerade g Zeilenweise für x1, x2, x3 in Ebene E einsetzen

Schaubild für das Lösen der Koordinatenform bei Lagebeziehungen von Gerade und Ebene



Beispiele

Beispiel Nr. 1 Koordinatenform:

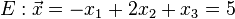
E: \vec x=-x_{1}+2x_{2}+x_{3}=5

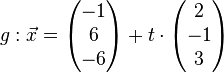
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right)

Die Gerade g Zeilenweise für x1, x2, x3 in Ebene E einsetzen

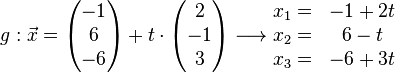
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right)\longrightarrow \begin{matrix} x_{1}= & -1+2t \\ x_{2}= & 6-t \\ x_{3}= & -6+3t \end{matrix}

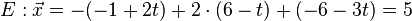
E: \vec x= -(-1+2t) + 2 \cdot (6-t) + (-6-3t) = 5
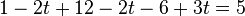
             1 - 2t + 12 - 2t - 6 + 3t= 5
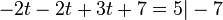
                  -2t - 2t + 3t + 7= 5 | -7
                           -t = -2
                            t = 2

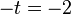
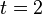
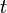t in Gerade g einsetzen:
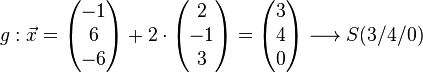
g: \vec x= \left( \begin{matrix} -1\\6\\-6 \end{matrix}\right) + 2 \cdot \left( \begin{matrix} 2\\-1\\3 \end{matrix}\right) = \left( \begin{matrix} 3\\4\\0 \end{matrix}\right) \longrightarrow S(3/4/0)

Beispeil Nr. 2 Parameterform:

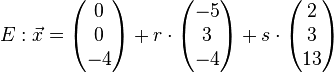
E: \vec x= \left( \begin{matrix} 0\\0\\-4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\-4 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)

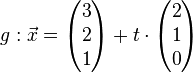
g: \vec x= \left( \begin{matrix} 3\\2\\1 \end{matrix}\right)+t \cdot \left( \begin{matrix} 2\\1\\0 \end{matrix}\right)

Auf "parallelität" überprüfen:
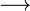\longrightarrow Normalenvektor von Ebene E ausrechnen
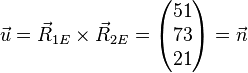
\vec u= \vec R_{1E} \times \vec R_{2E} = \left( \begin{matrix} 51\\73\\21 \end{matrix}\right)= \vec n

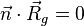
\vec n \cdot \vec R_{g}= 0
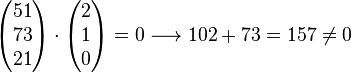
\left( \begin{matrix} 51\\73\\21 \end{matrix}\right) \cdot \left( \begin{matrix} 2\\1\\0 \end{matrix}\right) = 0 \longrightarrow 102+73= 157 \ne 0

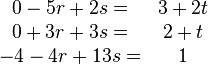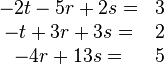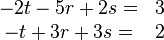
Ergebnis ist ungleich 0, also das LGS lösen: \begin{matrix} 0-5r+2s= &3+2t \\ 0+3r+3s= &2+t \\ -4-4r+13s= &1 \end{matrix}.............. \begin{matrix} -2t-5r+2s= &3 \\ -t+3r+3s= &2 \\ -4r+13s= &5 \end{matrix}.............. \begin{matrix} -2t-5r+2s= &3 \\ -t+3r+3s= &2 \end{matrix}

Aufgaben

Nr. 1 Parallelität

Zeige, dass die Gerade h parallel zur Ebene E ist.

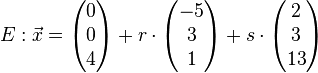
E: \vec x= \left( \begin{matrix} 0\\0\\4 \end{matrix}\right)+r \cdot \left( \begin{matrix} -5\\3\\1 \end{matrix}\right)+s \cdot \left( \begin{matrix} 2\\3\\13 \end{matrix}\right)

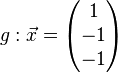
g: \vec x= \left( \begin{matrix} 1\\-1\\-1 \end{matrix}\right)




Nr. 2 Parallel, identisch oder Schnittpunkt

Untersuche ob Ebene E und Gerade g sich schneiden. Ist dies nicht der Fall, überprüfe ob g und E identisch sind oder parallel.

a.)
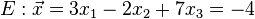
E: \vec x= 3x_{1}-2x_{2}+7x_{3}=-4

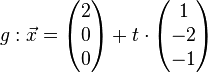
g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\-2\\-1 \end{matrix}\right)





b.)
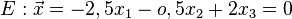
E:\vec x=-2,5x_{1}-o,5x_{2}+2x_{3}=0

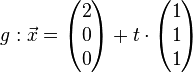
g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\1\\1 \end{matrix}\right)
br />






c.)
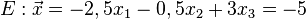
E: \vec x=-2,5x_{1}-0,5x_{2}+3x_{3}=-5

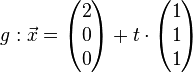
g: \vec x= \left( \begin{matrix} 2\\0\\0 \end{matrix}\right)+t \cdot \left( \begin{matrix} 1\\1\\1 \end{matrix}\right)




d.)
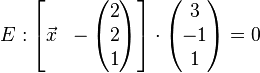
E: \begin{bmatrix} \vec x & -\left( \begin{matrix} 2\\2\\1 \end{matrix}\right) \\ \end{bmatrix} \cdot \left( \begin{matrix} 3\\-1\\1 \end{matrix}\right) =0

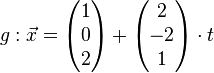
g: \vec x= \left( \begin{matrix} 1\\0\\2 \end{matrix}\right)+\left( \begin{matrix} 2\\-2\\1 \end{matrix}\right) \cdot t








e.)
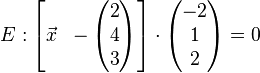
E: \begin{bmatrix} \vec x & -\left( \begin{matrix} 2\\4\\3 \end{matrix}\right) \\ \end{bmatrix} \cdot \left( \begin{matrix} -2\\1\\2 \end{matrix}\right)=0

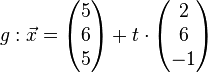
g: \vec x= \left( \begin{matrix} 5\\6\\5 \end{matrix}\right) + t \cdot \left( \begin{matrix} 2\\6\\-1 \end{matrix}\right)







f.)
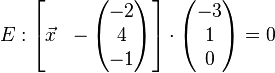
E: \begin{bmatrix} \vec x & -\left( \begin{matrix} -2\\4\\-1 \end{matrix}\right) \\ \end{bmatrix} \cdot \left( \begin{matrix} -3\\1\\0 \end{matrix}\right)=0

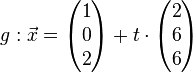
g: \vec x= \left( \begin{matrix} 1\\0\\2 \end{matrix}\right) + t \cdot \left( \begin{matrix} 2\\6\\6 \end{matrix}\right)





Nr. 3 Schnittpunkt

Untersuche die gegenseitige Lage von Ebene E und Gerade g.

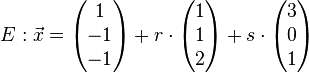
E: \vec x= \left( \begin{matrix} 1\\-1\\-1 \end{matrix}\right) +r \cdot \left( \begin{matrix} 1\\1\\2 \end{matrix}\right) +s \cdot \left( \begin{matrix} 3\\0\\1 \end{matrix}\right)

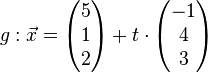
g: \vec x= \left( \begin{matrix} 5\\1\\2 \end{matrix}\right) +t \cdot \left( \begin{matrix} -1\\4\\3 \end{matrix}\right)










MeJvzm-fsg (Diskussion) 14:00, 18. Sep. 2016 (CET) M.Entenmann

Von „http://fsg.zum.de/index.php?title=Lagebeziehungen_zwischen_Gerade_und_Ebene&oldid=1692“