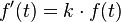Exponentielles Wachstum: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
(Die Seite wurde neu angelegt: „Exponentiell ist ein Wachstum, wenn ein Bestand in gleichen Zeitabständen um einen bestimmten Faktor zu- oder abnimmt.<br /> ==Funktionsgleichung== ===Funkti…“) |
K |
||
| Zeile 3: | Zeile 3: | ||
==Funktionsgleichung== | ==Funktionsgleichung== | ||
===Funktionsterm=== | ===Funktionsterm=== | ||
| − | Im Funktionstern steht <math>{a}</math> für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{t=0}</math>.<br /> | + | Im Funktionstern steht <math>{a}</math> für den Anfangsbestand, also den Bestand zum Zeitpunkt <math>{t=0}</math> .<br /> |
<math>{k}</math> steht für den Wachstums- beziehungsweise Zerfallsfaktor. Dieser bestimmt einerseits, wie stark oder schwach das Wachstum ist und andererseits ob es sich um Wachstum oder Zerfall handelt.<br /> | <math>{k}</math> steht für den Wachstums- beziehungsweise Zerfallsfaktor. Dieser bestimmt einerseits, wie stark oder schwach das Wachstum ist und andererseits ob es sich um Wachstum oder Zerfall handelt.<br /> | ||
<math>{t}</math> wird anstelle des <math>{x}</math> verwendet.<br /><br /> | <math>{t}</math> wird anstelle des <math>{x}</math> verwendet.<br /><br /> | ||
| Zeile 11: | Zeile 11: | ||
Die dazugehörige Differenzialgleichung lautet:<br /> | Die dazugehörige Differenzialgleichung lautet:<br /> | ||
<math>{f'(t)=k \cdot f(t)}</math><br /><br /> | <math>{f'(t)=k \cdot f(t)}</math><br /><br /> | ||
| − | + | Erklärung:<br /> | |
Die Ableitung des Funktionsterms lautet:<br /> | Die Ableitung des Funktionsterms lautet:<br /> | ||
<math>{f'(t)=k \cdot a \cdot e^{k \cdot t}}</math><br /> | <math>{f'(t)=k \cdot a \cdot e^{k \cdot t}}</math><br /> | ||
| − | Bis auf den Wachstumsfaktor <math>{k}</math> ist die Ableitungsfunktion <math>{f'(t)}</math> identisch mit der Ausgangsfunktion <math>{f(t)}</math>, daher kann der Teil ersetzt werden:<br /> | + | Bis auf den Wachstumsfaktor <math>{k}</math> ist die Ableitungsfunktion <math>{f'(t)}</math> identisch mit der Ausgangsfunktion <math>{f(t)}</math>, daher kann der identische Teil ersetzt werden:<br /> |
<math>{f'(t)=k \cdot f(t)}</math> | <math>{f'(t)=k \cdot f(t)}</math> | ||
Version vom 30. August 2018, 12:53 Uhr
Exponentiell ist ein Wachstum, wenn ein Bestand in gleichen Zeitabständen um einen bestimmten Faktor zu- oder abnimmt.
Funktionsgleichung
Funktionsterm
Im Funktionstern steht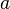 
für den Anfangsbestand, also den Bestand zum Zeitpunkt 
.
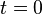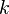steht für den Wachstums- beziehungsweise Zerfallsfaktor. Dieser bestimmt einerseits, wie stark oder schwach das Wachstum ist und andererseits ob es sich um Wachstum oder Zerfall handelt.
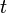wird anstelle des 
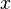verwendet.
Der sich daraus ergebende Funktionsterm lautet:
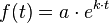
Differienzialgleichung
Die dazugehörige Differenzialgleichung lautet:
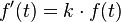
Erklärung:
Die Ableitung des Funktionsterms lautet:
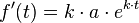
Bis auf den Wachstumsfaktor 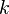ist die Ableitungsfunktion 
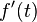identisch mit der Ausgangsfunktion 
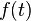, daher kann der identische Teil ersetzt werden:
