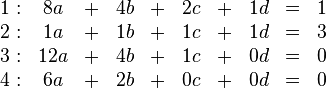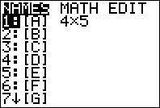Gauß-Algorithmus: Unterschied zwischen den Versionen
| Zeile 15: | Zeile 15: | ||
Gegeben sind die Funktionen: | Gegeben sind die Funktionen: | ||
| − | <math>\begin{ | + | <math>\begin{matrix} |
1.&3a+2b+1c=6\\ | 1.&3a+2b+1c=6\\ | ||
3.&-4c=20\\ | 3.&-4c=20\\ | ||
| − | 2.&2b-3c=11 | + | 2.&2b-3c=11 |
| − | end{ | + | \end{^matrix}</math> |
Formt man diese nun zu einer Dreiecksgestalt um, trägt dies sehr zur Übersichtlichkeit bei. | Formt man diese nun zu einer Dreiecksgestalt um, trägt dies sehr zur Übersichtlichkeit bei. | ||
| − | <math>\begin{matrix}1.&3a&+&2b&+&1c&=&6\\2.&&&2b&-&3c&=&11\\3.&&&&-&4c&=&20\end{matrix}</math> | + | <math>\begin{matrix} |
| + | 1.&3a&+&2b&+&1c&=&6\\ | ||
| + | 2.&&&2b&-&3c&=&11\\ | ||
| + | 3.&&&&-&4c&=&20 | ||
| + | \end{matrix}</math> | ||
Noch übersichtlicher wird es wenn man die Gleichungen in eine Stufenmatrix schreibt. | Noch übersichtlicher wird es wenn man die Gleichungen in eine Stufenmatrix schreibt. | ||
Version vom 6. März 2012, 18:04 Uhr
Inhaltsverzeichnis |
Wozu braucht man den Gauß-Algorithmus?
Der Gauß Algorithmus ist ein Verfahren zur Lösung von linearen Gleichungssystemen beliebig vieler Variablen und beliebig vielen Gleichungen.
Lineare Gleichungssysteme können genau eine, keine oder unendlich viele Lösungen haben.
1 - Wenn nur eine Lösung vorhanden ist, hat die Stufenform die Gestalt eines Dreiecks.
2 - Das lineare Gleichungssystem hat unendlich viele Lösungen, wenn es eine oder mehrere Zeilen gibt, in denen nur Nullen stehen.
3 - Hat das lineare Gleichungssystem in einer Zeile auf der linken Seite nur Nullen stehen und auf der rechten Seite auf der gleichen Zeile eine Zahl ungleich Null ist, gibt es keine Lösung.
Um die Lösung leicht zu bestimmen werden die Gleichungssysteme in der sogenannten Stufenform (=Dreiecksform) angeordnet.
Anzuwenden ist er beispielsweise bei folgender Situation:
Gegeben sind die Funktionen:
Fehler beim Parsen(Unbekannte Funktion „\end“): \begin{matrix} 1.&3a+2b+1c=6\\ 3.&-4c=20\\ 2.&2b-3c=11 \end{^matrix}
Formt man diese nun zu einer Dreiecksgestalt um, trägt dies sehr zur Übersichtlichkeit bei.
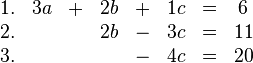
Noch übersichtlicher wird es wenn man die Gleichungen in eine Stufenmatrix schreibt. (näheres bei Lösen ohne GTR)
Nun kann man dieses Gleichungssystem nach und nach lösen.
Berechnung ohne GTR
Gegebenes Gleichungssystem:
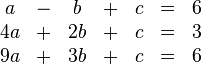
Ziel: Um die unbekannten Variablen herauszufinden, rechnen wir mit der Form einer Stufenmatrix.
Ziel dabei ist es, in der ersten Zeile keine Null, in der zweiten Zeile an erster Stelle eine Null und in der dritten Zeile an den ersten zwei Stellen jeweils eine Null zu bekommen.
So sollte es am Ende aussehen:
| a | b | c | |
|---|---|---|---|
| 1 | -1 | 1 | 6 |
| 0 | -6 | 3 | 21 |
| 0 | 0 | -2 | -6 |
Erlaubt sind:
1. Multiplikation/ Division einer Zeile mit einer Zahl, die nicht Null ist.
2. Vertauschen zweier Zeilen miteinander.
3. Zwei Zeilen miteinander/ voneinander addieren/ subtrahieren.
Beispiel:
Anwendung mit Hilfe des GTR
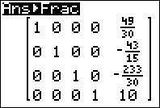
Mit einem grafikfähigen Taschenrechner oder einem Computer-Algebra-System lässt sich die Lösungsmenge eines LGS (Lineares Gleichungssystem) schnell bestimmen. Dazu gibt man die "erweiterte Koeffizientenmatrix" mithilfe des Matrix-Editors ein. Das Gleichungssystem wird in eine Matrix übertragen. Dazu benötigt man den GTR:
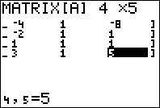
Schritt 1:
2nd → Matrix → Edit:
Zahlen eingeben
2nd → Quit
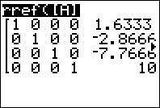
2nd → Matrix → Math → rref(
2nd → Matrix → [A] → Enter
Jetzt kann man aus der Koeffizientenmatrix das Ergebnis direkt ablesen.
Anwendungsbeispiele
Kaffeemischung aus drei verschiedenen Kaffeesorten
30px Aufgabe
Eine Kaffeerösterei bietet drei verschiedene Kaffeemischungen an. |
Lösung:
| Marke | Brasilien | Kolumbien | Mexiko | Preis für 5kg |
| Mocca | 1 | 3 | 1 | 63 |
| Barry | 2 | 1 | 2 | 66 |
| The Dark One | 3 | 1 | 1 | 67 |
Die Aufgabe wurde mit dem oben beschriebenen Lösungsweg gelöst.
Ein Kilogramm brasilianischen Kaffees kostet 13€.
Ein Kilogramm kolumbianischen Kaffees kostet 12€.
Ein Kilogramm mexikanischen Kaffees kostet 14€.
Steckbriefaufgabe
30px Aufgabe
Gesucht ist eine ganzrationale Funktion mit den Eigenschaften: |
Lösung:
Nebenbedingungen(entnehmbar aus der Aufgabenstellung):
| 1. | 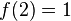
|
(P) |
| 2. | 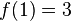
|
(Q) |
| 3. | 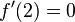
|
(Extrempunkt bei P) |
| 4. | 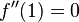
|
(Wendepunkt bei Q) |
Aufstellung der allgemeinen Funktionsgleichung:
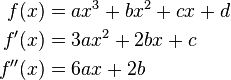
Jede aufgestellte Nebenbedingung definiert eine Variable der Funktion.
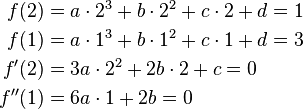
GTR → Matrix berechnen
4x5 Matrix: