Lagebeziehungen zwischen Ebene und Ebene: Unterschied zwischen den Versionen
Aus Friedrich-Schiller-Gymnasium
| Zeile 15: | Zeile 15: | ||
<math>E_2:-x_1 + 2x_2 -3x_3 = 4</math> | <math>E_2:-x_1 + 2x_2 -3x_3 = 4</math> | ||
| − | <math> | + | <math>E_3:-6 x_1 + 4x_2 -2x_3 = 1</math> |
<math>E_4:-3 x_1 + 2x_2 -x_3 = -4</math> | <math>E_4:-3 x_1 + 2x_2 -x_3 = -4</math> | ||
{{Lösung versteckt mit Rand| | {{Lösung versteckt mit Rand| | ||
| − | 1=Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E<sub>1</sub> und E<sub>3</sub>), sonst sind sie identisch (Ebenen E<sub>1</sub> und E<sub>4</sub>). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E<sub>2</sub> mit allen anderen Ebenen. | + | 1=Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E<sub>1</sub> und E<sub>3</sub>), sonst sind sie identisch (Ebenen E<sub>1</sub> und E<sub>4</sub>). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E<sub>2</sub> mit allen anderen Ebenen). |
<math> \vec n_1= \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) </math>, | <math> \vec n_1= \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) </math>, | ||
| Zeile 27: | Zeile 27: | ||
<math> \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) </math>. | <math> \vec n_4= \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) </math>. | ||
| − | <math> -2 \cdot \vec n_1= -2 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) | + | <math> -2 \cdot \vec n_1= -2 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -6\\4\\-2\end{matrix}\right) = \vec n_3</math>, aber <math>-2 \cdot 4 \neq 1</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| + | <math> -1 \cdot \vec n_1= -1 \cdot \left( \begin{matrix} 3\\-2\\1\end{matrix}\right) = \left( \begin{matrix} -3\\2\\-1\end{matrix}\right) = \vec n_4</math>, aber <math>-1 \cdot 4 = -4</math> | ||
}} | }} | ||
Version vom 25. September 2012, 11:19 Uhr
|
Lernpfad
|
Beide Ebenen in Koordinatengleichuing gegeben
30px Aufgabe
Welche der Ebenen E1, E2, E3, E4 sind zueinander parallel? |
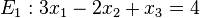
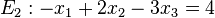
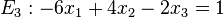
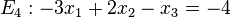
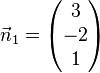 ,
,
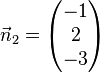 ,
,
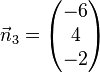 ,
,
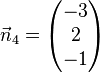 .
.
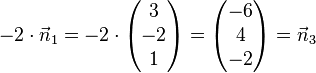 , aber
, aber 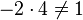
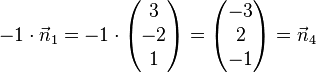 , aber
, aber