Lagebeziehungen zwischen Ebene und Ebene
|
Lernpfad
|
Beide Ebenen in Koordinatengleichuing gegeben
30px Aufgabe
Welche der Ebenen E1, E2, E3, E4 sind zueinander parallel? |
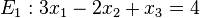
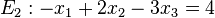
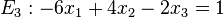
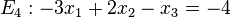
Lösung: Es müssen die Normalenvektoren der Ebenen untersucht werden. Sind diese linear abhängig, dann sind die Ebenen parallel oder identisch. Sind jetzt die Ebenengleichungen keine Vielfache, dann sind die Ebenen parallel (Ebenen E1 und E3), sonst sind sie identisch (Ebenen E1 und E4). Sind die Normalenvektoren linear unabhängig, schneiden sich die Ebenen (Ebene E2 mit allen anderen Ebenen).
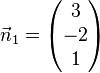 ,
,
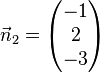 ,
,
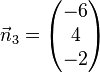 ,
,
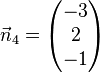 .
.
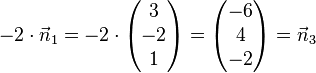 , aber
, aber 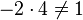
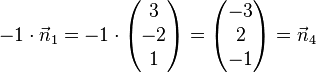 , aber
, aber 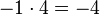
Somit lässt sich eine Vorgehensweise verallgemeinern, mit der man die Lage zweier Ebenen untersuchen kann, indem man die Normalenvektoren untersucht und eventuell noch die gesamte Gleichung betrachtet.
30px Aufgabe
Erstelle ein Baumdiagramm als Arbeitsanweisung zur Untersuchung der Lage zweier Ebenen, die durch eine Koordinatengleichung gegeben sind. |
<graphviz>
digraph G {
"ZUM-Wiki-Rundgang" -> "Was ist ein Wiki?";
"ZUM-Wiki-Rundgang" -> "Das ZUM-Wiki";
"ZUM-Wiki-Rundgang" -> "Probier es aus!";
"Probier es aus!" -> "Ich will im Wiki schreiben.";
"Probier es aus!" -> "Ich will im Wiki etwas finden.";
"Probier es aus!" -> "Wiki-Fuehrerschein";
"ZUM-Wiki-Rundgang" -> "Wikis in der Schule?";
}
</graphviz>

