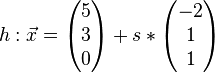Winkelberechnungen zwischen Geraden und Ebenen
Schnittwinkel zwischen zwei Geraden
Wenn sich zwei Geraden schneiden, entstehen vier Winkel, zwei mit 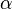 (
(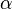
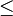 90°)und zwei mit 180°-
90°)und zwei mit 180°-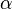 .
Der Schnittwinkel der beiden Geraden ist der Winkel, der kleiner oder gleich 90° ist. Wenn
.
Der Schnittwinkel der beiden Geraden ist der Winkel, der kleiner oder gleich 90° ist. Wenn 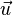 und
und 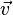 Richtungsvektoren sind, kann man den Schnittwinkel
Richtungsvektoren sind, kann man den Schnittwinkel 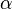 mit der folgenden Formel berechnen: cos(
mit der folgenden Formel berechnen: cos(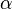 )=
)= 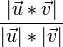
Beispielaufgabe:
Gegeben: 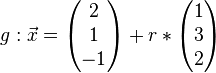
Gesucht: Schnittwinkel 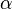
cos()=
=
Schnittwinkel
= 70,9°
Schnittwinkel zwischen zwei Ebenen
Der Schnittwinkel 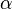 zwischen zwei Ebenen ist der Schnittwinkel zweier Geraden g und h, die in einer der beiden Ebenen liegen und orthogonal zu der Schnittgeraden s der Ebenen sind. Der Schnittwinkel
zwischen zwei Ebenen ist der Schnittwinkel zweier Geraden g und h, die in einer der beiden Ebenen liegen und orthogonal zu der Schnittgeraden s der Ebenen sind. Der Schnittwinkel 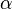 wird mit der folgenden Formel berechnet, da dieser Winkel dem Winkel zwischen den Normalvektoren
wird mit der folgenden Formel berechnet, da dieser Winkel dem Winkel zwischen den Normalvektoren 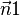 und
und 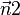 der Ebene gleich ist.
cos(
der Ebene gleich ist.
cos(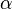 )=
)= 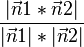
Beispielaufgabe:
Geg.: 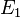 :
: 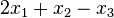 =12
=12
:
=0
Ges.: Schnittwinkel 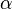
cos()=
=
Schnittwinkel
= 42,4°
Schnittwinkel zwischen einer Geraden und einer Ebene
Wenn man das Lot einer Geraden g auf die Ebene E fällt, erhält man in der Ebenen eine Gerade g'.Der Winkel der zwischen der Geraden g und g' gibt den Schnittwinkel 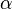 der Geraden g und der Ebene E an. Der Winkel
der Geraden g und der Ebene E an. Der Winkel 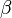 zwischen dem Normalenvektor
zwischen dem Normalenvektor 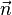 der Ebene E und dem Richtungsvektor
der Ebene E und dem Richtungsvektor 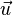 der Geraden g ergänzt den Schnittwinkel
der Geraden g ergänzt den Schnittwinkel 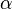 zu 90°.
sin(
zu 90°.
sin(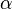 )=
)= 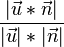
Beispielaufgabe:
Geg.: 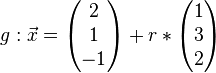
:
=12
Ges.: Schnittwinkel 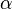
sin()=
=
Schnittwinkel
= 19,1°
Abstand zwischen windschiefen Geraden
Der Abstand zwischen zwei windschiefen Geraden ist die kleinste Entfernung zwischen den Punkten von den Geraden g und h.
Wenn G bzw. H Punkte auf den Geraden 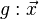 =
=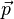 +s*
+s*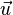 bzw.
bzw. 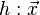 =
=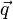 +t*
+t*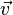 sind, dann gilt:
sind, dann gilt:
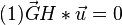 und
und
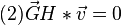 ,
dann ist
,
dann ist 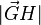 der Abstand der beiden Geraden g und h.
der Abstand der beiden Geraden g und h.